To part 1 of "Gravitation as a pressure force..."

To part 2 of "Gravitation as a pressure force..."

To part 4 of “Gravitation as a pressure force…”

Here: “Gravitation as a pressure force…”, part 3 = Section 7

7. Gravitationally-modified Maxwell equations and their link to photon trajectories

As emphasized by Will [40], any viable theory of gravitation should be "complete", in the sense that it should match with the whole of physics. However, even GR does not match with quantum physics, because a consistent theory of "general relativistic quantum gravity" does not exist yet, in fact it is not sure that such theory is still expected seriously. Hence, accounting for the present state of physics, a reasonable demand of completeness is that, in addition to a mechanics, an alternative theory of gravitation should involve also a description of the electromagnetism in the presence of gravitation [40]. This description should lead to a set of "gravitationally-modified" Maxwell equations, and a further requirement is that these modified equations should be consistent with the geometrical optics of the theory as defined by the trajectories of light-like particles. In other words, the theory should tell us how the electromagnetic rays may be defined from some particular electromagnetic waves, and it should prove that these rays do move as light-like particles do it under the gravitation. In GR and other metric theories, the modification of the Maxwell equations is rather easy, because it is an application of the well-known rule "comma goes to semi-colon": due to the commonly accepted formulation of Einstein's equivalence principle, one just has to substitute the curved physical metric g for the flat one into the covariant expression of any law of non-gravitational physics. (However, this rule is generally ambiguous when the expression contains higher-order derivatives. So in the case of Maxwell's equations, one is carefully warned not to apply the rule to the equations for the potential, and instead to apply the rule to the equations for the field tensor F.) Further, in GR and other metric theories, the transition from wave optics to geometrical optics is most rigorously made with the help of the discontinuities equations for an electromagnetic shock wave, with the result that the electromagnetic rays are the bicharacteristics of Maxwell's equations, corresponding to "null" fields, and following light-like geodesics (cf. e.g. Synge [37]).

In the present theory, the electromagnetic field tensor F is stated to derive from a 4-potential in the usual way: in particular it is antisymmetric, F_mn = - F_nm , and the first group of the Maxwell equations is satisfied,

F_{lm ,n} + F_{mn , l} + F_{nl ,m} = F_{lm ;n} + F_{mn ; l} + F_{nl ;m} = 0. (46)

However, we cannot use the "comma goes to semi-colon" rule, because this theory is not a metric theory (although it does endow the space-time with a curved physical metric g). Specifically, the form of the second group of Maxwell's equations in metric theories,

(47)

(where J ^µ is the 4-current), implies that, in vacuo, the energy-momentum tensor of the electromagnetic field,

T _field ^mn º (- F ^m _l F ^nl + g ^mn F _lr F ^lr )/4p, (48)

obeys Eq. (24), instead of Eq. (37) - and Eqs. (24) and (37) are equivalent only for a constant gravitational field. In the proposed theory, the Maxwell equations are obtained as an application of Newton's second law for a charged dust subjected to the gravitation force and to the Lorentz force. Hence, we begin with a short outline of continuum dynamics in the presence of gravitational and non-gravitational forces [8]. Just the same method of induction from a dust to a general continuum is used as in Sect. 6, the difference being that now the dust particles are subjected, in addition, to a non-gravitational external force. The density f of the latter is assumed given, and is expressed in terms of the physical volume measure dV = Ög dx ¹ dx ² dx ³ (with g º det (g_ij)). Thus, the non-gravitational external force over a volume element of the dust is

d F₀ = f dV. (49)

(In accordance with the spirit of field theory, the particles are still assumed to not interact directly: instead, their presence produces a field that exerts a force on them. This is more intuitive with the concept of a space-filling fluid ether, of course.) Adapting the energy equation (28) and then the expression (36) of the 4-acceleration for an individual particle to the situation with a non-gravitational force, and using the same method as in Sect. 6, one gets

, , (50)

where b ^µ (T) is the vector deduced from the covector (38) by raising up the indices with g.

The expression of the Lorentz force on a point particle with charge q may be derived uniquely from the requirements that (i) it must be an invariant space vector by the group (7), and (ii) this vector must reduce to the classical expression in the absence of gravitation (in Galilean coordinates for the flat metric g = g ⁰),

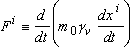
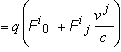. (51)

By this method, the expression of the Lorentz force in the presence of gravitation is found to be [8]

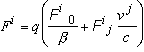
. (52)

Considering then a continuous medium (a "charged dust"), we define r_el º dq/dV and J ^µ º r_el dx ^µ/dt_x. The density of the Lorentz force is written, in accordance with Eqs. (49) and (52), as

. (53)

The charged dust obeys the equation for continuum dynamics in the presence of gravitation and the Lorentz force, Eq. (50) with f given by Eq. (53). On the other hand, the total energy-momentum is the sum T = T_dust + T_field , and this total tensor must obey the equation for continuum dynamics in the presence of gravitation and without any non-gravitational external force, Eq. (37). Due to the linearity of the expression (38) of b ^µ as a function of T, it follows that the energy-momentum tensor of the electromagnetic field must satisfy

, . (54)

In words: the electromagnetic field may be considered as a "material" continuum subjected to the gravitation and to the opposite of the Lorentz force. This gives the gravitational modification of Maxwell's second group in the present theory. Indeed, Eq. (54) may be rewritten as

(55)

and this, in the case of an invertible 4-4 matrix (F ^m _n ), may in turn be written in the form

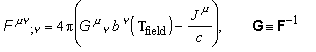. (56)

Equation (56) is what corresponds, in the present theory, to Eq. (47) of GR, and it reduces to Eq. (47) for the case of a constant gravitational field (in the preferred frame). The condition det F ¹ 0 is equivalent to E.B º - e ^mnry F_mn F_ry /8 ¹ 0, it is hence satisfied by "generic" electromagnetic fields. However, it is not satisfied by the simplest examples of e.m. fields, i.e. purely electric fields, purely magnetic fields, and "simple" electromagnetic waves (also called "null fields"), for which fields one may use only the weaker equation (55). A striking consequence of Eq. (56) is that the electric charge is not conserved in a variable gravitation field, since Eq. (56) implies that

. (57)

However, it is difficult to give estimates without having recourse to a numerical work (in contrast to the situation for matter production, Sect. 6), hence this interesting and dangerous prediction is yet to be precised.

Equation (55) is sufficient to make the transition from wave optics to geometrical optics in the theory. The geometrical optics in vacuo is defined, in the present theory, as the study of the trajectories of light-like particles, which are ruled by the proposed extension (19) of Newton's second law, without any non-gravitational force, thus F₀ = 0 in Eq. (19). As we have seen, the modified second group of the Maxwell equations, Eq. (55) or Eq. (56), is just the expression of Newton's second law for that continuous medium which is defined by the energy-momentum tensor of the electromagnetic field. In vacuo, a volume element of the field continuum will be subjected to the gravitation and, in general, to internal forces exerted by the neighbouring elements. Therefore, the condition F₀ = 0, which must apply to an isolated photon, has to be replaced by the double condition that (i) the field continuum is subjected to zero non-gravitational external force, i.e., f = 0 in Eq. (50), and (ii) it is subjected to zero internal force. Condition (ii) means that the continuum behaves like a dust (a dust of photons), i.e., that its energy-momentum tensor has the form

T ^mn = V ^m V ⁿ. (58)

One may indeed show that, independently of the exact physical nature of the material or field, Eq. (58) is the necessary and sufficient condition ensuring that any volume element of the continuum is subjected merely to the gravitation and to the non-gravitational external force density f, thus with zero internal force [8]: in that case, the spatial part of the dynamical equation of the theory, Eq. (50)₂, is equivalent to

f dV + g = , (59)

where the purely material energy of the element is defined, consistently with Eqs. (29) and (30), as

dE = de _m/b = T ⁰ ₀ dV ⁰ /b = T ⁰ ₀ dV, (60)

and where the absolute velocity of the element, u = dx/dT , is defined by

u ⁱ º c T ⁱ ₀/T ⁰₀, (61)

which is the velocity of the flux of the total matter energy, as Eq. (31) shows.

Now, in the case of the energy-momentum tensor of the electromagnetic field (Eq. (48)), condition (ii) turns out to be equivalent to saying that the e.m. field is a null field (with both invariants equal to zero), whereas, due to Eqs. (53) and (54), condition (i) is equivalent to J ^µ = 0, i.e. to the requirement that an "empty" domain is considered (i.e. a domain in which the e.m. field is the only form of "matter"). Thus, a "dust of free photons" is exactly a null field in vacuo. Furthermore, for a such field, the second group of Maxwell's equations is Eq. (55) with J ^µ = 0, which is equivalent to Eq. (54) with f = 0, hence this group is equivalent to the dynamical equation for the electromagnetic dust in vacuo:

, . (62)

As we have recalled above, Eq. (62)₂ may be rewritten, for a null field, as

g = , (63)

where u _field is defined by Eq. (61), thus

u _field ⁱ º c T _field ⁱ ₀/T _field ⁰₀

[and with

dE _field º T _field ⁰ ₀ dV ,

Eq. (60)]. This definition of u _field, together with Eq. (58) and the fact that T _field has zero trace, imply that

|v_field| = c

[8]. This and Eq. (63) allow us to conclude: in the case of a null field in vacuo, each trajectory of the e.m. energy flux is a photon trajectory of the present theory, as defined by Eq. (19) for a free light-like particle (F₀ = 0). This is the link between wave optics and ray optics in the proposed theory.

To part 4 of “Gravitation as a pressure force…”