Gravitation as a pressure
force: a scalar ether theory
Proc. 5th. Int.
Conf. " Physical Interpretations of Relativity Theory " (London, 1996), Supplementary Papers Volume
(M.C. Duffy, édr.), British Soc. Philos. Sci./ University of Sunderland, 1998, pp.
1-27.
This
web page: Part 1 = Sections 1 to 4 of the paper
Mayeul Arminjon
Laboratoire
"Sols, Solides, Structures", Institut de Mécanique de Grenoble
B.P. 53, 38041 Grenoble Cedex
9, France
1. Introduction and summary
The concept of an
ether means primarily that empty space does not really exist. We may believe
this, for instance, because electromagnetic waves, that go accross
intergalactical space, ought to wave in some medium. We may also believe this,
because quantum phenomena, such as the Casimir effect, suggest that
"vacuum" actually has physical properties. It has been established by
Builder [10-11], Jánossy [20-21], Prokhovnik [33-34], and others, that the
concept of the ether as an inertial frame which should be the carrier of the
electromagnetic waves (the Lorentz-Poincaré ether), is fully compatible with
Special Relativity (SR). In connection with this, Zhang [41] has recently
reestablished, against contrary statements, that the one-way velocity of light
cannot be consistently measured – in the absence of any faster information
carrier. As emphasized by Duffy [17], the Builder-Prokhovnik reconstruction of
standard SR from the Lorentz-Poincaré ether concept may be criticized on the
ground that this construction makes undetectable the absolute reference frame
and its velocity, which are the physical entities with which the construction
starts. It would not be an appropriate answer to recall that, after all, this
is the way in which Lorentz, Larmor and Poincaré themselves derived the major part
of SR: indeed, this methodological oddness – which is not a logical fault,
however – contributed to bring discredit on the ether concept for a long time.
Another possible answer would be to insist that, beyond physical concepts, one
may still introduce metaphysical ones.
The answer that will be suggested here
is, instead, that SR does not rule the whole of physics, for it does not
involve gravitation. If the presence of a gravitational field breaks the
symmetry expressed by the Lorentz group, then the Lorentz-Poincaré construction
of SR is justified as the examination of a particular physical situation, the
general situation (with gravitation) being one in which the "absolute
motion" should be detectable. Although it is admittedly a risk to build a
preferred-frame theory of gravitation, it will be shown that the risk is
smaller than one would think, if one would blindly follow the standard
arguments. Moreover, there are well-known physical reasons that may justify to
search for a radical alternative to general relativity: e.g. the singularity
occuring during gravitational collapse, the problem of dark matter, and the
questions about the influence of the gauge condition.
The theory summarized here starts from
a tentative interpretation of gravity as a pressure force, which would give a
new theory already in a Newtonian space-time ; this will be recalled in Section 2. However, to become
compatible with SR, this interpretation of gravity calls for a new version of
Einstein's equivalence principle, which consists in admitting that our physical
standards of space and time are affected by gravitation in much the same way as
they are affected by a uniform motion (Section
3). Yet in the "pseudo-Riemannian space-time" which is thus
obtained, motion is governed by an
extension of Newton's second law, instead of assuming Einstein's motion
along geodesic lines of the space-time metric (Section 4). The extended Newton law implies an energy balance for a
test particle moving in a variable gravitational field; this balance equation
may be translated so as to apply to a dust, of course (dust is a continuum made
of non-interacting particles). The field equation of the theory allows to
rewrite the balance equation for a dust as a true conservation equation for the total energy, including the
gravitational energy; this conservation equation is then assumed valid for any
kind of material or non-gravitational field, characterized by its
energy-momentum tensor (Section 5).
Using a different method, one may obtain the 4-component equation governing the
dynamics of a dust continuum in terms of the energy-momentum tensor; this
equation also may be assumed to be valid for any continuum, it is the
substitute for the classical equation T mn ; n = 0 of general relativity and other metric theories. The new equation
implies that mass conservation is
obtained as a limit behaviour for a weak and slowly varying gravitational field
and/or at low pressure (Section 6).
The same method as in Sect. 6 may be used in the presence of a field of (non-gravitational)
external force. When the external force is the Lorentz force, the 4-component
dynamical equation thus derived gives the second group of the gravitationally-modified Maxwell equations,
in the investigated theory. This new modification of Maxwell's equations is consistent with the geometrical optics of
the theory as governed by the proposed extension of Newton's second law (Section 7). An essential question is whether the theory agrees with experiment or
not, of course. The theory has the correct Newtonian limit; it predicts
Schwarzschild's exterior metric of general relativity and geodesic motion in
the static situation with spherical symmetry. Therefore, the question amounts
principally to assessing the preferred-frame effects. To do this, one must
develop a "post-Newtonian" approximation of this non-linear theory (Section 8). The first result is that no preferred-frame effect occurs for photons
at the (first) post-Newtonian approximation. However, the absolute velocity
of the solar system does influence the motion of mass points at this same
approximation, thus it does have to be accounted for in celestial mechanics,
according to the present theory. But it will be argued, contrary to well-known
arguments, that the existence of
preferred-frame effects in celestial mechanics, comparable in magnitude with
the "relativistic" effects, does not a priori invalidate a theory.
2. Semi-heuristic considerations and a theory for Newtonian absolute
space and time
Our
starting point is that the concept of an ether should first be made compatible
with classical mechanics [1]. This is
not so easy: on the one hand, within classical mechanics, the only medium that
could "fill the vacuum without us feeling it", would be a perfect
fluid, which indeed would not brake any motion. But, on the other hand, we want
that the ether defines an inertial frame, for otherwise we would have to
postulate both an ether and an independent absolute space, and it seems that
this would be too much of "absolute". (Moreover, the ether defines an
inertial frame in the Lorentz-Poincaré interpretation of SR, although obviously
this argument is less closely related to classical mechanics.) Hence, in the
case of usual Newtonian mechanics, our perfect fluid should be perfectly rigid!
The proposed answer is that it is the
average motion of the perfect fluid that defines the preferred inertial frame
[1-2] (the average should be taken at a very large scale, formally it is the
asymptotic volume average [4]). It is worth to note that, even if one remains
within classical mechanics, thus with our physical standards being assumed to
measure Euclidean distance and absolute time, this preferred inertial frame
does not actually need to be rigid. In other words, Newtonian mechanics may be
extended to deformable inertial
frames: the only restriction, imposed by the principle of inertia, is that the
motion of the inertial frame with respect to a (any) rigid reference frame
should be irrotational [1]. This generalization allows some simple cosmological
considerations, in particular it gives a simple argument for an expanding
universe [1]. An expanding preferred frame was already envisaged by Prokhovnik
[33-34]. The motion (deformation) of the preferred inertial frame E, thus the average motion of
the fluid ether, does not obey this "neo-classical" mechanics, since
this average motion defines the frame of this mechanics. (It means that this
mechanics does not say us whether E has a rigid motion, an expansion, or any other
irrotational motion: we have to empirically determine this motion. Note that
the "neo-classical" mechanics is the usual classical mechanics only
in the case that the frame E has a rigid motion with respect to a (any)
rigid reference frame.)
However, we may tentatively assume
that the microscopic motion of the
(micro-)ether with respect to its mean
rest frame E or macro-ether, does obey mechanics, as well as the motion of material
particles. The micro-ether being a perfect fluid, it exerts only surface forces
due to its pressure, which may be reexpressed as volume forces depending on the
gradient of the pressure of the micro-ether. Thus, any material,
"elementary" particle, supposed to occupy a finite volume, is
subjected to this Archimedes thrust, just like a ball in the sea (in this
tentative reasoning, we deliberately "forget" the fact that quantum,
not classical mechanics, is usually admitted to apply at this scale). In order
that this pressure force be a universal force depending only on the inertial
mass of the material particles, it is sufficient to assume that the mass
density inside any particle (averaged over the volume of the particle) is the
same for all particles, say rp. Then a field 
of "ether
pressure" would give the gravity acceleration
g = – (grad 
) /rp
[1, 3]. (It turns out that
this interpretation of a universal gravitation force was proposed by Euler in
1746! See Whittaker [39].) We then note that rp may still depend on 
, but on 
only, and that this
would seem miraculous unless the material particles themselves are made of the
hypothetical fluid – as is also suggested by the unity of matter and fields,
and by the observed transformations of particles into different ones. According
to this notion of a "constitutive ether", material particles would be
organized local flows in the ether, which seems a very promising heuristics as
regards the realistic interpretation of these objects of microphysics - as shown
in detail by Romani [35]. Hence, we equate rp to 
, the local "density" of the micro-ether, which
must depend on 
only, i.e. a
barotropic fluid (this is necessarily the case for a perfectly continuous fluid,
for which entropy and temperature do not make sense [35]). We thus assume that
g = – (grad 
) /
. (1)
It
is worth noting that Eq. (1) implies a decrease
of the ether pressure 
and the ether density
= 
(
) in the direction of the gravitational attraction. Because
the gravitation varies only over macroscopic distances, 
must be the
macroscopic pressure in the ether; more precisely, grad 
must be the average of grad 
over a macroscopic volume, with 
the "true"
microscopic pressure of the ether [1]. This leaves the possibility that the
other interactions, which vary over much shorter length scales, could be
explained as combined effects of the field 
on the matter
particles, the latter being seen as organized flows. We see that gravitation
can be envisaged as a correction
defined by Eq. (1), even in the case where the "mass density inside a
matter particle" would not be the same for all particles. In other words,
at the scale of the elementary particles, the universality of the gravitation
force might be a question of definition. Moreover, the sequel of the
development of the theory (Sect. 3) leads to admit that the compressibility of
the (micro-)ether is K = 1/c 2 with c the velocity of light, thus an
extremely low compressibility. In this situation, it is natural to expect that
the mass density is indeed nearly the same for all particles.
Equation (1), thus obtained
semi-heuristically, is yet assumed to be an exact equation of the theory, which
is a substitute for the Newtonian equation g
= grad U.
In a phenomenological point of view, "a theory is defined by the set of
its equations" (as Hertz said about Maxwell's electromagnetic theory). The
next step is to state the equation relating the field of macroscopic ether
pressure, 
, to the mass density r (the latter is, of course, the usual density, r = dm/dV, with dm the sum of the masses of the material particles involved in some volume
element dV ). To do this, we assume, as did Romani [35], that Newtonian gravitation
(NG) corresponds to the limit case of an incompressible fluid. Indeed,
gravitation propagates instantaneously in NG, whereas, if gravitation is a
pressure force, it should propagate with the "sound" velocity in the
fluid ether,
, (2)
which
is infinite only for an incompressible fluid. In order to recover Poisson's
equation for the gravity acceleration g
(Eq. (1)), the field equation must be in the incompressible case:
Dpe = 4p G r re. (3)
In
the static situation, the propagation speed plays no role; it is thus natural
to assume that, in the static situation, this same equation still applies also
in the case where the fluid indeed has a compressibility. However, this means
already a new, non-linear theory of gravitation, implying e.g. a perihelion
shift for the orbit of a test particle in a static field with spherical
symmetry [1]. In assuming that the ether is conserved, that the wave motion of
the ether with respect to its mean rest frame obeys Newton's second law, and by
adapting standard arguments of acoustics, one then finds that the field
equation of the general case is [1]
Dpe 
= 4p G r re. (4)
Thus,
the concept of a fluid ether leads quite naturally to the notion that gravitation
should propagate in essentially the same way as the most usual waves, i.e.
acoustic and electromagnetic waves. Equation (4) is not Galileo-invariant,
hence this theory with Newtonian space-time is a preferred-frame theory. NG and
Galilean invariance are recovered as the limit case of an incompressible fluid.
3. Principle of equivalence between the metric effects of uniform motion
and gravitation
The
foregoing theory has to be adapted so as to account for the
"relativistic" effects, here seen as resulting from the
"real" Lorentz contraction [10-11, 20-21, 33-34]. Thus, these effects
are essentially absolute metric effects of uniform motion. Einstein's principle
of equivalence between inertial effects and effects of a true gravitational
field is an extrapolation of a ("weak") principle of equivalence,
valid in Newtonian theory as a simple consequence of the identity between
inertial mass and passive gravitational mass. As it has been often discussed in
the literature (see e.g. Fock [18]), these equivalence principles are valid
only in an infinitesimal domain, such that the gravitational field, as well as
the field of "fictitious" inertial forces due to the motion of the
considered frame with respect to the inertial frame, may be considered as uniform.
Now, in a relativistic theory, the infinitesimal domain must be in space-time,
so that the uniformity should be true both in space and in time. But, in an
infinitesimal domain of space-time, any motion may be considered as uniform,
and a uniform motion can have none other effect as the metric effects due to
the FitzGerald-Lorentz contraction of the measuring rods and the
Larmor-Lorentz-Einstein dilation of the clock periods. Hence, we are lead to
the conclusion that, if there can be an equivalence principle, this should give
the correspondence between the metric effects of a uniform motion and certain
metric effects that should appear as a consequence of a (locally) uniform
gravitational field.
Under our assumption that a
gravitational field is due to a variation in the ether pressure, or
equivalently in the ether density, we indeed can see an analogy between a
uniform motion and a gravitational field: due to the Lorentz contraction, the
"apparent" density of the ether is modified by the uniform motion.
More precisely, let us assume that an observer following the uniform motion, at
constant velocity V with respect to
the macro-ether E, can use the "true" simultaneity (of the frame E), which he indeed can use
if he knows his absolute velocity V
– this, in turn, being a priori
possible in a preferred-frame theory which will lead to definite effects of the
absolute motion, at least in the presence of a gravitational field. Then, a
given volume dV 0 of ether (as evaluated with
the rods of E) has, for this observer, a greater volume dV = dV 0/bV,
with
bV = (1 – V 2/c 2)1/2,
because
his measuring rod is contracted in the ratio bV in the direction V. The
"mass" or rather the amount of ether is unchanged, for the mass increase
with velocity concerns only material particles. Hence, due to the absolute
motion, the
apparent ether density is lowered, re V = re .bV. Now the metric effects of uniform motion depend only on bV, thus they depend only on the ratio between the "apparent"
density which might be "evaluated" by the moving observer, and the
"true" density that he might evaluate if he were not in a motion: bV = re V /re < 1. Similarly, a
gravitational field implies that the local ether density re is
lower (see after Eq. (1)) than the ether density re¥ in remote regions that are free from gravitation. We are thus naturally
lead to postulate that [2-3]:
(A) In a gravitational field, material objects
are contracted, only in the direction of the field g (with g = - (grad pe)/re ), in the ratio
b = re / re¥ < 1 , (5)
where re¥ is the ether density at a
remote point where no gravity is present, and the clock periods are dilated in
the same ratio.
This
statement is made for objects and clocks bound with E ; if this is not so, one has to combine the
metric effects due to motion and gravitation. Due to the contraction of
measuring rods in the direction g,
the physical space metric g in the frame E becomes
a Riemannian one. The contraction of the rods (hence the dilation of the
measured distances) occurs with respect to a "background" Euclidean
metric g0, which is assumed to be bound with the macro-ether E. The latter assumption
means that the components g0ij are constant in coordinates bound to the
preferred frame - i.e., space-time coordinates (x
µ )µ = 0,
... , 3, such that each point bound to E has constant space
coordinates (x i ) i = 1, 2, 3. [1] In the same way, the dilation of the clock periods implies a
contraction of the local time interval dtx, measured with a fixed
clock (bound to E) in a gravitational field, as compared with the corresponding interval
of the "absolute time", dT,
thus
dtx/dT = b. (6)
This
assumption (A) gives a specific form to the space-time metric g [2]. In particular, the
slowing down of clocks, as expressed by Eq. (6), implicitly assumes that the
absolute time T is a globally synchronized time coordinate
[23] in the frame E, i.e., the components g0i are zero in coordinates (x µ ) that
are bound to the preferred frame and such that x 0 = cT,
which means that a simultaneity is defined in the frame E as a whole [3, 5]. The property "g0i = 0" holds true after any coordinate transformation
of the form
x' 0 = f (x 0), x' i = y i (x
1, x 2, x 3).
(7)
These
transformations, that both leave the frame unchanged and keep true the global
synchronization [5], build a group which is important in the theory [7-8].
However, in order that the time-dilation (6) be univoquely defined, it is
necessary to restrict oneself to the subgroup constituted by the merely spatial
transformations [7-8]; this justifies the term "absolute time" for T. Note that T is the time which is measured by a clock bound to the preferred
frame and far enough from massive bodies so that no gravitational field is
felt.
The author recently learned that a
somewhat similar equivalence principle between metric effects of uniform motion
and gravitation had previously been assumed, in the special case of a static
gravitational field, by Podlaha & Sjödin [30] (cf. also Podlaha [29] and Sjödin [36]). However, the assumption of
these authors is different from assumption (A) hereabove: the ratio assumed by
Podlaha & Sjödin is b' = (r0/r)1/2, where r0 is
the ether density in an unaffected region and plays thus the same role as our re¥, so that one might
write b = 1/b' 2 if the "ether density" re (or
r for Podlaha and Sjödin) were one and the same
field in both approaches. Yet for Podlaha & Sjödin [30], the ether density increases in the direction of the
gravitational attraction, this increase being approximately determined by the (opposite of the) Newtonian
potential, -U = - GM/r for the static field
produced by a spherical body with mass M
: their equation (20) amounts to r/r0 = (1 - U/c 2)-2, or b' = 1-U/c 2. For a weak gravitational field, our assumption (A) gives b » 1 - U/c 2 [2], thus b » b' for a weak
field. However, our assumption is stated for any gravitational field, and even
for a weak field there are correction terms [6] (see Eq. (64) here). We have
given a heuristic justification for assumption (A) (see also Refs. 2-3).
Another difference is the way in which the spatial contraction is assumed to
occur, i.e., whether it is isotropic or not: Podlaha & Sjödin do not
precise this point, but Eq. (8) in Podlaha [29] seems to imply that the
contraction would be locally isotropic. According to our hypothese, the spatial
contraction is anisotropic (just like the FitzGerald-Lorentz contraction),
since it occurs in the direction of the g
vector only.
As a result of the proposed
equivalence principle, two different space metrics, g and g0, as
well as two different times (the local time tx and the absolute time T ), might be used by observers bound to
the preferred frame. Combining the space and time evaluations into a space-time
metric (which, in contrast, is valid for any observer in any reference frame),
we may also say that we have two such metrics on the "space-time": an
"abstract" one, g 0, obtained by combining g0 and T, and which is flat, and
a "physical" one, g, obtained by combining g and tx, and which is curved. The question then arises as to
which metric we should refer the equations for the field of ether pressure,
Eqs. (1) and (4). We assume that, due to the local character of these two
equations, and for yet another reason, the physical
space and time metrics must be used [2-3]. This means (i) that the gradient
operator in Eq. (1), as well as the Laplace operator in Eq. (4), are given by
(grad f)i = (gradg f )i = gij 
, (gij) º (gij)-1,
(8)
D f = Dg f = divg gradg f = 
, g º det (gij); (9)
and
(ii) that the time derivative in Eq. (4) must be understood as relative to the
local time tx, that is
. (10)
Now
the "sound" velocity in the ether, ce, depending on the local ether density pe as given by Eq. (2), must
be assumed to be equal (everywhere and at any time) to the constant velocity of
light c [2]. This can be true only if
pe = c 2
re + a, and the constant a must be zero since the pressure must
cancel for nil density, thus we get: pe
= c 2 re . The modification of Eq. (4) accounting for SR and the equivalence
principle is hence written as
. (11)
In
this equation, r is now "the mass-energy
density", a somewhat ambiguous expression to be precised in Section 5.
Using assumption (A), one may rewrite Eq. (1) [now valid with the gradient
defined in terms of the curved physical metric g, Eq. (8)] and Eq. (11) in terms of the
Euclidean metric g0 and the absolute time T [4]:
=
(g00)E , (x 0 = cT ), (12)
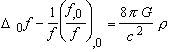, D0 º Dg0 º divg0 gradg0 , (x 0 = cT ). (13)
However,
Eq. (13) is equivalent to Eq. (11) only if the "reference ether
pressure" pe¥ is
time-independent, i.e., the universe is assumed "static at infinity",
which may indeed be assumed, except for cosmological problems [4]. The simple
form (12)-(13) of the main equations has important computational consequences.
4. The motion of a test particle as defined by an extension of Newton's
second law
In
the investigated theory, the motion of mass points and light-like particles, as
well as the motion of any continuous medium (Sections 6 and 7), is governed by
an extension of Newton's second law to curved space-time. The main reason to
seek after such an extension was that Einstein's assumption, according to which
free test particles follow space-time geodesics, gives a physical status to
space-time. That the primary object of physics should be such mixture of space
and time, is very difficult to accept for the "common sense", and has
puzzling consequences such as the possibility of a travel back in time, with
its well-known paradoxes. In contrast, if the Lorentz-Poincaré interpretation
of SR is adopted, the space-time may be envisaged simply as a (very convenient
and clever) mathematical tool. This is indeed the way in which Poincaré [31]
introduced in 1905 the concept of the space-time as a 4-dimensional space with
coordinates x, y, z, ict. According to the view adopted here,
the "relativistic space-time couplings" are merely due to physical
effects, on clocks and meters, of absolute motion and gravitation. Einstein's
geodesic assumption could be compatible with this view only in the case that
this assumption could be deduced from another one, directly compatible with the
notion of distinct space and time. Such is Newton's assumption "Force = time-derivative of momentum".
In classical mechanics, it is indeed
possible to rewrite Newton's second law, in a force field deriving from a constant potential, as the geodesic equation
for a certain artificial space-time metric, and this exactly (cf. Mazilu
[25]). In relativistic gravitation theory, it is known to be possible,
conversely, to rewrite the spatial part of the geodesic equation as Newton's
second law, again in the case of a constant
gravitational field, i.e. for a time-independent space-time metric [23].
However, Landau & Lifchitz [23] did not actually prove that the obtained
Newton law, thus three scalar equations, is equivalent to the geodesic equation, which involves four scalar equations. In the case of a variable
metric, the various attempts to rewrite the geodesic equation with
frame-dependent gravitational forces have been reviewed by Jantzen et al. [22]. As it appears from their
review, and as it is also discussed in Ref. 5, none of these attempts is fully
convincing. The reason is, in the author's opinion, that most of these
researchers did not try to play the game "Newton's second law" with
an equivalent equipment to that in
classical mechanics, thus one reference frame (of which the possible changes
may be discussed, if desired, in a subsequent
step), with one spatial metric and one measure of physical time (Møller
[27] did try this, but his pioneering proposal has one serious shortcoming, to
be recalled hereafter). Instead, most authors retain the whole of the
space-time metric with its ten independent components – in contrast with the
seven scalars involved in the spatial metric (six) plus the local time (one).
To get a real, compelling equivalent
of Newton's second law in a given reference frame, in the
"relativistic" situation where the spatial metric g is curved by gravitation
and evolves with time, and where
clocks go differently at different places and times, is the objective that, the
author believes, has been reached by the following proposal [4-5].
i) The precise expression of the force
F will depend, of course, on each
particular theory, and will be decomposed into a non-gravitational
(non-universal) force F0,
whose expression should be adapted from SR, and a gravitational force Fg. The universal character
of the latter, plus the assumption that SR must hold true locally, impose that
it has the form Fg = m(v) g, where m(v) is the relativistic inertial mass,
m(v) º m(v = 0).gv º m(0).(1-v 2/c
2)-1/2, (14)
the
velocity vector v and its modulus v being evaluated in terms of the local
physical standards of space and time,
v
i º dx i/dtx , v º [g(v, v)]1/2
= (gij v i v j)1/2, (15)
and
where g is a space vector that should
depend only on the current position and velocity of the test particle. The
dependence on the velocity may be surprising at first if one remembers
Newtonian gravity, but it means simply that the gravity acceleration g may contain an inertial part – as is
to be expected if a general reference frame is considered. Even in a general
reference frame, the data of the space-time metric determines uniquely the
increment of the local time, dtx ("synchronized"
along the trajectory of the test particle, cf.
Cattaneo [13] and Landau & Lifchitz [23]). This means that the ratio dtx/dc, with c the parameter used to run along the
trajectory, is unambiguously defined once a fixed reference frame is considered
[5]. In the present theory, the preferred frame E is a globally synchronized
reference frame (i.e., the g0i components are zero, e.g. with the choice x 0 = cT for the time coordinate). This implies that the trajectory may
always be parametrized with the absolute time T (which is also true for any
other globally synchronized coordinate time, T ' = f(T )), and that the relevant
ratio is very simple, Eq. (6).
ii) There is no choice for the expression of the momentum , i.e. the product of the inertial mass and the velocity:
P º m(v) v. (16)
The
difficult point is definition of the time-derivative
of the momentum along the trajectory. Indeed, to define this consistently, we
have to define, more generally, the derivative of any vector w(c) on the trajectory (defined by the dependence x i = x i(c)), and this trajectory is in a space (3-dimensional manifold) equipped
with a Riemannian metric g that varies with the parameter c along the trajectory. The variation referred
to is not merely the spatial variation in g (or in its components gij ) as the point x = (x i ) is changed (this variation is usual for a
Riemannian manifold). It is also the time variation, precisely it is the fact
that the spatial field g (the correspondence between
any spatial point x' and the local metric g(x')), is not the same for different values of the parameter c (which indeed plays the
role of a time).
The first difficulty, i.e. the spatial
variation of the metric, has been solved since a long time, and it is for this
reason that the case of a constant gravitational field has been solved also:
the correct time-derivative of a vector w(c) along a trajectory in a
space equipped with a fixed
Riemannian metric, is what is usually called the absolute derivative D0w/Dc (relative, however, to the
considered metric g and to the considered parameter c ; of course, if one changes c to x = x(c), one gets D0w/Dx = (dc/dx)D0w/Dc ). The absolute derivative is usually
introduced as a by-product of the "covariant derivative", the latter
being valid for fields defined in volume domains of the manifold (e.g.
Brillouin [9], Lichnerowicz [24]). However, the absolute derivative may be
introduced specifically as the only consistent time-derivative of a vector
along a trajectory, in the case of a fixed metric [2]. (Of course, the absolute
derivative may be defined for manifolds with an arbitrary number of dimensions:
e.g. in the case of the 4-dimensional space-time, the absolute derivative with
respect to the space-time metric g and to the parameter s = c t with t the proper
time, DW/Ds, allows definition of the 4-acceleration of a
test particle, A º DU/Ds with U º dx/ds the
4-velocity.)
In order to define the
time-derivative D w/Dc of a vector w(c) along a trajectory x(c), in the case of a variable
metric field g = gc , we impose the following essential requirements [5]: 1) it must be a
space vector depending linearly on w;
2) it must reduce to the absolute derivative if g does not depend on c ; 3) it must be expressed in terms of the space
metric g and
its derivatives; and 4) it must obey Leibniz' derivation rule for a scalar
product, i.e.
.
(17)
It
turns out that these requirements allow to define one and only one
time-derivative, given by [5]:
D w/Dc º D0w/Dc + (1/2) t.w, t º 
. (18)
In
particular, Leibniz' rule (17) is responsible for the unique possible value of
the coefficient multiplying the vector t.w = (t i j w j ), i.e. l = 1/2. In contrast, Møller's definition of Newton's second law [27]
amounts to using the value l = 0, i.e. to take the absolute time-derivative relative to the frozen space metric of the
"time" c0 where the derivative is to be calculated;
thus, this time-derivative does not
obey Leibniz' rule with the actual, variable metric, Eq. (17). Leibniz' rule is
very important to obtain correct energy equations [4-5].
Now, to write Newton's second law in
terms of local standards, the parameter c must be the local time tx,
"synchronized" along the trajectory. Moreover, one defines naturally
for a mass particle the "purely material" energy (i.e., not
accounting for the potential energy in the gravitational field [4]) as E º m(v)c 2, so we finally write:
F0 + (E/c 2) g = D P/Dtx .
(19)
iii) For a light-like particle (photon, neutrino?), the energy E of the particle (or rather the ratio E/c 2 i.e. the mass
equivalent of the energy) plays the role of the inertial mass [13], so we
define
P º (E/c 2) v, (20)
it
being understood that E is the usual, "purely material"
energy, related to the frequency n by Planck's relation
E = hn (21)
(here
n is the frequency as measured with the local
time, i.e. by the momentarily coincident clock). Equations (19) and (20) define
one and the same Newton law for both mass particles and light-like test
particles. Furthermore, the frequency n deduced from E by Eq. (21) is none other
than de Broglie's frequency [30].
iv) Having thus defined a
unique extension of Newton's second law, Eq. (19), to any space-time curved by
gravitation, a question naturally arises: is this extended Newton law
compatible with geodesic motion? Since geodesic motion applies only to free particles, we have to investigate
the case F0 = 0 in Eq. (19); and since the gravity acceleration g has not been defined in the general statement of Newton's second
law (although it is defined, in our theory, by Eq. (1) or equivalently by Eq.
(12)), it is clear that the question can be reformulated thus: which form of the gravity acceleration g is
compatible with Einstein's geodesic motion? Recall that Eq. (19) can be
written in any reference frame (although the transformation law of g from one frame to another one has not
been given, and does not seem to be easy to get: g is only assigned to be a spatial vector in a given reference
frame). As in Newtonian theory, one may expect that the form of g should be simpler is some special
class of reference frames. It turns out that the "convenient" frames
are the "globally synchronized "
ones, i.e. frames such that, in certain coordinates bound to the frame, the g0i components are zero. This is not surprising in this
"neo-Newtonian" approach: in general frames, the time can be
synchronized only on a trajectory, whereas the notion of a global simultaneity
is essential (perhaps the most essential notion at all) in classical mechanics.
According to Landau & Lifchitz [23], the very existence of globally
synchronized frames is a property valid for generic space-times. However, there
are "pathological" space-times in which it is not valid. The answer
to the above question has been found [5] for such generic space-times:
In order that free particles
follow space-time geodesics, it
is necessary and
sufficient that, in
any globally synchronized reference frame, the gravity acceleration have the following expression:
,
. (22)
v) It is seen that the
"Einsteinian" gravity acceleration, Eq. (22), differs from the gravity acceleration assumed in the present theory
by the second, velocity-dependent term in the right-hand side: this term is
absent from Eq. (1), whereas, due to the equation pe = c 2 re (see
after Eq. 10), the first term in the r.h.s. of Eq. (22) is just the r.h.s. of
Eq. (1). Note that the velocity-dependent term cancels for a gravitational
field that is constant in the considered frame. Therefore, another question
arises: how to phenomenologically
characterize the assumed gravity acceleration, Eq. (1) with pe = c 2re? The answer is [5]:
Assume that in some "globally synchronized" reference frame F (g0i = 0), the gravity acceleration be a space vector g depending only on the
metric field g. More precisely, assume
that g does
not depend on the time variation of
g and is linear with respect
to the space variation of g. In order that free particles
follow space-time geodesics in the static case (gmn , 0 = 0), it is necessary and
sufficient that the general expression of vector g in the frame F be
,
(23)
with g the space metric in F.
This result characterizes
the assumed field g independently of
any heuristic consideration on the ether. The assumption that the metric field g is a "spatial potential"
for the field g is natural if one
wants to account for the equivalence principle without going too far from
Newtonian theory. Thus, Einstein's geodesic motion would be valid only in a
static gravitational field.
to part 2 of "Gravitation as a pressure force..."
To part 3
of “Gravitation as a pressure force...”