To part 1 of "gravitation as a pressure force..."
To part 3 of “Gravitation as
a pressure force...”
To part 4 of “Gravitation as a pressure force…”
Here: “Gravitation as a pressure force…”, part 2 = Sections 5 and 6
of the paper
5. Energy balance and energy conservation
We summarize the discussion
in Ref. 4, where a few additional references are discussed. The concept of
energy is an essential one in most of modern physics but, surprisingly, it can
hardly be defined in modern gravitation theory, i.e. in general relativity
(GR). Indeed, an extremely important feature of the energy is that it should be
conserved, also locally, in the sense that a local balance equation without
any source term should apply to the total energy. Now according to GR and
other relativistic theories of gravitation based on general covariance plus
Einstein's "equivalence principle" (in the standard form: "in a
local freely falling frame, the laws of non-gravitational physics are the same
as in SR"), the general "conservation equation" is the equation
(T mn
; n ) µ = 0, ..., 3 º divg T = 0 (24)
for the energy-momentum tensor T [2].
But, as emphasized in most textbooks on GR, e.g. Landau & Lifchitz [23],
this equation can not be considered as a true conservation equation (a balance
equation without source term), for there is no Gauss theorem applying to the
divergence of a second-order tensor in a curved Riemannian space. (In turn the
main reason for this is that one can simply not define the integral of a vector
field in a such space.) In more explicit terms: one cannot rewrite Eq. (24) in
the form of a true conservation equation which would be valid for a generic
coordinate system, i.e., which would be consistent with the principle of
general covariance. One may, however, rewrite Eq. (24) in the form of a true
conservation equation, if one accepts to restrict oneself to coordinate systems
exchanging by linear coordinate transformations,
as are Lorentz transformations in a flat space-time. Unfortunately, one may do
this in many different ways, so that it is not clear which would be the correct
way, even once one has specified the linear class of coordinate systems. Moreover,
there is no reason to introduce such particular class, unless "the
space-time has a particular symmetry", which means in fact that some background metric g0 on the
space-time manifold, distinct from the physical metric g, has some non-trivial group
of isometries. The example of a such background metric that is relevant to the
rewriting of Eq. (24) as a true conservation equation is that of a flat metric [4]: a such metric admits a
particular class of coordinate systems, in which it reduces to the Galilean
(Minkowskian) form. In summary, the search for a consistent concept of energy
leads in GR to a contradiction with the very notion of "general
relativity", since this search leads to restrict oneself to reference
frames exchanging by Lorentz transformations of a flat background metric. In
the present preferred-frame theory, on the other hand, we do have a flat
background metric g0 and we do not
even demand that the energy balance equation should be covariant by Lorentz
transformations of this flat metric, so it would be hard to accept that the
theory would not lead to a true conservation equation for the energy.
The obtainment of the energy equation for a mass point (pp.
42-43 in Ref. 4) is a modification of the elementary method used in classical
mechanics to derive the energy equation in a force field deriving from a
variable potential (the modifications are due to relativistic mechanics with a
variable metric). Here, the assumed expression for g (Eq. 23)) derives from the potential U ' º - c 2 Log b. Thus, one
evaluates the rate of work per unit rest mass for a "free" mass
point,
= gv g.(dx/dtx) = c
g.(dx/ds) (25)
(where the point means
scalar product g), using Newton's second law (19) (with F0 = 0), which
involves the correct time-derivative (18). The result is
.
(26)
Using the definition of the
potential U ', one rewrites this as
, (27)
or, multiplying by m0c 2 with m0
the rest mass:
. (28)
Equation (28) shows clearly
that the total energy of the mass point must be defined as
e m º Eb = c 2m0gv b, (29)
which is a constant for a constant
gravitational field. This is the total energy of the mass point, for it
includes both its "purely material" energy E (i.e. the energy equivalent of the relativistic inertial mass,
thus including the "kinetic" energy) and its "potential"
energy in the gravitational field, which may be defined as e gm = em - E =
E (b - 1). (It is hence negative, as
in NG.) It turns out that just the same equation (28) may be derived also for a
light-like particle.
The deduction of the energy equation (28) from Eq. (27) is
trivial, but it rests on the essential assumption that the rest mass m0 of the free mass point is
conserved in the motion (an assumption that is already used in the derivation
of Eq. (26)). If we now consider a dust,
i.e. a continuum made of coherently moving, non-interacting particles, each of
which conserves its rest mass, we may apply Eq. (27) pointwise in the
continuum. The conservation of the rest-mass of the continuum is most easily
expressed in terms of the "background" Euclidean metric g0 and the
associated volume measure dV 0, for it is then
expressed as the usual continuity equation for the density of the rest-mass
with respect to dV 0, which is r00 º dm0/dV 0. The density, with respect
to dV 0, of the total energy of the dust, is e m º c 2r00gv
b, because
d e m = c 2dm0 gv b = c 2r00 dV 0 gv
b = e m dV 0. (30)
It turns out that e m is none other
than the T 0 0 component of the
energy-momentum tensor T for the
dust, whose T i 0 components are T i 0 = T 0 0 u
i/c, with u i º dx i /dT the
"absolute velocity" (with respect to the preferred frame, and
evaluated with the absolute time T ) [3].
Using this and rewriting Eq. (27) with the help of the continuity equation, one
gets the local balance equation for the
continuum:
(x
0 = cT ),
(31)
where the identity applies
when the spatial coordinates in the preferred frame are Cartesian (at least at
the point considered), i.e. such that g 0ij = dij and g 0ij, k = 0.
To rewrite this as a true conservation equation, we must
use the field equation of the theory (Eq. (13)) so that the r.h.s. of Eq. (31),
which in this form is a source term, be recast as a 4-divergence with respect
to the flat metric g0. In other words,
we have to make the gravitational energy and its flux appear. To do this, we
adapt the reasoning that leads to a conservation equation in NG: we observe
that, due to Eqs. (12) and (13), one has [4]
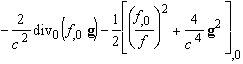, div0 º div g0, g2
º g0(g, g), x
0 = cT . (32)
On the other hand, using the
condition g0i = 0, the r.h.s. of Eq. (31) may be rewritten as [4]
. (33)
Since c 2r is "the
mass-energy density" (in the preferred frame), it should be equal to T
00, or to T 0 0, or still to T 00. But Eqs.
(32) and (33) show that the source term on the r.h.s. of Eq. (31) can be
rewritten as a flat 4-divergence, if and only if c 2r = T
00. Therefore, we must precisely define c 2r as the T
00 component (in coordinates bound to the preferred frame, and
such that x 0 = cT ). This also means that the
gravitational field reinforces itself, whereas,
if
we would assume c 2r =T 00 or c 2r =T 00, the
gravitational field would have a weakening effect on itself [4]. We therefore
obtain the local conservation equation
for the continuum:
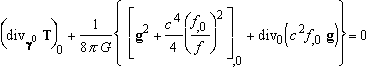(x 0 = cT ). (34)
Although this equation has
been derived for a dust, we assume that it holds true with T the total energy-momentum
tensor of any kind of continuum (involving material particles and/or
non-gravitational fields). This assumption is justified by the mass-energy
equivalence and the universality of the gravitation force. Equation (34) rules
the exchange between the total energy of matter, whose density is given by e m = T 0 0 (cf. Eq.
(30)), and the purely gravitational energy, whose density e g is defined by
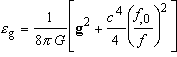. (35)
This exchange occurs through
the intermediate of the flux of the total matter energy, defined as the space
vector with components cT i 0, and the flux of
the gravitational energy, defined as the space vector c 3f , 0
g/(8 p G). Note that the total energy of matter
contains also the negative potential energy of matter (and/or non-gravitational
fields) in the gravitational field: for a dust, T 0 0
= e m is the density
of the total energy of the individual particles, defined by e m = c 2m0gv b (cf. Eqs. (29) and (30)).
Of course, the local conservation of the energy implies a global conservation
(of the global amount of total energy,
i.e. gravitational energy plus total energy of matter), under asymptotic
conditions ensuring that the global energy is finite [4].
6. Continuum dynamics and
matter creation/destruction
By the foregoing induction
(from a dust to a general continuum), we have got one scalar local equation for
a continuous medium, i.e. the energy conservation, which, for a general
continuum, is substituted for the mass
conservation. However, for a point particle, we have four equations: the
three equations of motion (19), plus the conservation of the rest-mass, and it
is easy to convince oneself that one also needs exactly four independent
dynamical equations for a continuum, in addition to the state equation. For
instance, there are indeed four dynamical equations in classical continuum
mechanics: Newton's second law plus the continuity equation. The same number
applies also in GR, where the dynamical equations make the well-known 4-vector
equation (24).
In order to get the required four scalar "equations of
motion" for a continuous medium, we may again use the general principle of
induction from a dust to a general behaviour, once the equation for dust has
been expressed in terms of the energy-momentum tensor T. The most expedient way to operate this principle turns out to be
passing through the expression of the 4-acceleration
[7]. The latter expression has been obtained for a free particle [5]. (The spatial
components of the 4-acceleration and its time component were deduced from
Newton's second law (19) and the energy equation (27), respectively, by using
the relation between the Christoffel symbols of the spatial metric and those of
the space-time metric.) It happens to be simpler in covector form 4 :
A 0 = 
, A i = -
. (36)
(By the way, Eq. (36) shows
at once that, in the present theory, Einstein's geodesic motion is recovered
only for a gravitational field that is constant in the preferred frame: A = 0 is true for
whatever 4-velocity U if and only
if gij, 0 =0.) For a dust,
the T tensor has the form T mn = c 2r* U m U n with r* the proper rest-mass
density, and, for any material continuum, the 4-acceleration may be expressed
as A m = U n U
m; n . Using this and
the mass conservation, assumed valid by definition for a dust, one may rewrite
Eq. (36), for a dust, as
, (37)
where bµ is defined
by
, 
. (38)
Now the induction principle
means simply that Eq. (37) is the general equation for continuum dynamics
in the present theory. It thus plays the role played in GR by Eq. (24). The
r.h.s. of Eq. (37), bµ as
defined by Eq. (38), is a 4-covector for transformations of the group (7), and
so is also Eq. (37). The time component of Eq. (37) (µ = 0) is equivalent to the energy balance equation (31), hence
also to the energy conservation equation (34) [7]. Moreover, for a dust, i.e.
the case T mn = c 2r* U m U n, Eq. (37) implies
the mass conservation, i.e.
, (39)
and (again for a dust), Eq.
(37) implies also the expression (36)
for the 4-acceleration, which is characteristic for free motion in the present
theory, i.e. F0 = 0 in Newton's
second law (19) [7]. Thus, Eq. (37) plus the relevant definition of the
energy-momentum tensor as a function of the state variables (which, for dust,
consist of the single variable r*) characterize
completely the dynamical behaviour of dust. This is an important consistency
test.
A
general continuum may thus be phenomenologically defined by the expression of
tensor T as a function of some state
variables, and Eq. (37) determines how the continuum couples to gravitation in
the present theory (of course, Eq. (37) reduces to the equation valid in SR,
i.e., T m n, n = 0, if there is no gravitational field). But, for a
general continuum, the energy is conserved,
and this is in general incompatible with
the exact mass conservation: in the case of a variable gravitational field,
there are exchanges between the gravitational energy and the total energy of
matter, so one may a priori expect that, in general, the rest-mass will not be
conserved - except for the
special case of a dust. One may already verify this for the simple case of a
perfect isentropic fluid. The energy-momentum tensor of a perfect fluid is
in general
T
fluid mn = (m*
+ p)
U m
U n
-
p
g mn , (40)
with p
the pressure and µ* the volume
density of the rest-mass plus internal energy in the proper frame: in energy
units,
m*
º r*( c 2 + P), (41)
where P is the internal
energy per unit rest mass. For a perfect fluid, the isentropy condition is
simply
d P + p d(1/r*) = 0. (42)
For instance, for a barotropic fluid, one
assumes m* = m*(p); then, r* and P also depend on p only, P being given by
[18]
P(p) º 
. (43)
Due to Eq. (43), a
barotropic fluid is automatically isentropic.
For any isentropic fluid, Eq. (37) leads to the following equation for mass creation/destruction:
= 
, (44)
which indeed shows that,
except for the limit case of a dust (p
= 0) and for the limit case of a constant
gravitational field (f , 0
= 0), the rest-mass is not conserved - according to the present
theory [7]. In contrast, GR and other relativistic theories are based on Eq.
(24), which, for an isentropic fluid, implies the conservation of the
rest-mass, Eq. (39) (cf.
Chandrasekhar [15]). On the contrary, the present theory predicts that matter
may really be produced or destroyed, due to the variation of the gravitational
field. Prigogine et al.
[32]
consider that matter should be produced by a such exchange (albeit in an
irreversible way, excluding matter destruction),
and this exchange would indeed seem a
priori natural in a theory with conserved energy, due to the mass-energy
equivalence. However, matter production can hardly happen so in GR: we insist
that, due to the equation for continuum dynamics that goes with geodesic
motion, i.e., T mn ; n
=
0, matter can only be produced if one phenomenologically inserts an additional
term, which is not determined by the
set of the state equation plus the Hilbert-Einstein equations [12, 19, 32].
Roughly speaking, this "creation term" appears thus as an ad hoc, adjustable source term, which is
used to allow production of matter in some cosmological models. It seems
interesting to investigate the possibility that matter might be produced (or destroyed ) by an exchange with the
gravitational field (a more complete discussion of this question is given in
Ref. 7, that includes in particular a discussion of the thermodynamical
constraints). Yet in our opinion, such exchange should not be considered merely
in a cosmological context, but actually for any gravitational field.
Precisely, the way in which matter production occurs in any
variable gravitational field, as implied by Eq. (44), may seem dangerous for
the present theory, because it would mean that matter is continuously produced
or wasted away under our eyes. However, the rates would be extremely small and
often the mean gain would be rather close to zero [7]. If the absolute velocity
V of the solar system is of the
order 300 km/s, the main contribution in Eq. (44) would come from that
variation of the gravitational field which is due to the translation of any
celestial body through the ether, giving a creation rate (the amount produced
per unit time in some material domain, divided by the mass of that domain)
C º 
(Vr º V. er ), (45)
with M and R the mass and
radius of the spherical celestial body, whose attraction g (g = GM/r 2 outside the body)
dominates in its near environment (er is the unit radial vector).
At a fixed point on the surface of a body in self-rotation (as it is indeed the
case for the planets), the corresponding contribution would be exactly cyclic
at the equator, and instead would constantly accumulate production of matter
(resp. destruction) at one pole (resp. at the other pole). Near the surface of
the Earth, for instance, the ratio p/(c 2r) can hardly take values
much higher than 10 - 12 (which is its
value in the air at the atmospherical pressure). A ratio equal to 10 - 12 leads to a
maximum value of the creation rate Cmax
» 3. 10 - 23 s- 1 (obtained for er
parallel to V, and with V » 300 km/s), which seems very
difficult to detect [7]. Hence, it might be the case that this new form of
energy exchange be a real phenomenon. Needless to emphasize, this would be
interesting.