To the References of the paper (= end of this page)

To the beginning of the paper

6. THE MODIFIED NEWTON LAW IMPLIES GEODESIC MOTION OF LIGHT-LIKE PARTICLES

A basic prediction of GR, also found with the ETG (Eq. (19)), is that clocks are slowed down in a gravitation field. One empirical confirmation is the observed gravitational red shift of electromagnetic spectra. To deduce the red shift from the slowing down of clocks, the frequency

n₀ of any monochromatic wave is considered constant throughout its light path, when expressed in terms of the time coordinate t - in the case of a stationary field where the space-time metric (g_ab) does not depend on t. This constancy of n₀ in turn is derived from the wave equation  f=0 with f=exp(iy), y=w(x¹,x²,x³)t + f(x¹,x²,x³) and  f from Eq. (24) : Laue proved this for a static field [17] but his arguments extend to a stationary one, in the way outlined in the treatise [18]. Laue [17] also deduced from the same way of reasoning that light rays follow the null geodesic lines of g . These arguments also apply in the ETG, since they depend only on the equation  f=0, in the limit of geometrical optics. It is, however, interesting to show that in the ETG the constancy of n₀ as well as the geodesic propagation can be deduced also from the modified Newton law (20) with the mass of the energy E in the place of the inertial mass m(u) :

in which n is the frequency as measured with the local (momentarily coinciding) clock, n=dn/dt_x , as imposed by the local nature of quantum phenomena (h is Planck's constant and n is the number of oscillations). The constancy of n₀ = dn/dt = (p_e/p_e0)n means that the energy of the photon decreases if it moves off from the attracting body, in such a way that :

E p_e = E₀ p_e0 = Const. along the light path. (31)

We first prove that for a static field (p_e time-independent), (31) follows from (30) and the fact that, as measured with physical clocks and rods (bound to E), the modulus of the velocity of the photon is always equal to c :

(the usual notations for scalar products and squares, u.v and u², refer to the curved space metric g). Combining (30)₁ and (32)₂ we get :

but according to Eq. (5) where the grad operator refers to the metric g and with p_e=r_ec², we have

g.dx = - (grad p_e . dx)/ r_e = - c² dp_e/p_e .

Therefore, (33) may be rewritten as

- E c² dp_e/p_e = c² dE , (35)

which means that d(Ep_e)=0 along the path, i.e. Eq. (31) is obtained.

Now we prove that Eqs. (30) and (31) imply that the photon moves along a null geodesic line of g (during this proof, we omit the index e in p and r for simplicity). Let x₀ be any fixed point in M (i.e. x₀ is at rest in the ether), outside the gravitation field (i.e. far enough). We introduce the universal time coordinate x⁰=ct with t=t_x0. Whether the field p depends on t or not, we may adopt, at any time t, a space coordinate system (xⁱ) on M such that p=Const. is equivalent to x¹=Const., and such that the Euclidean metric g⁰ is diagonal in the natural basis (e_i) :

(g⁰_ij) = diag ().

Then, assumption (A) and Eq. (16) with p=r c² mean that g also is diagonal, and that:

(g_ij) = diag 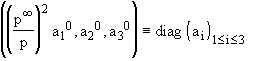, (36)

with p^¥ = p(x₀). In the case where such an "isopotential" coordinate system is bound to the frame E, the space-time metric (21) writes in the local coordinates (x^a) (a=0,3) of the space-time R´M:

(g_ab) = diag 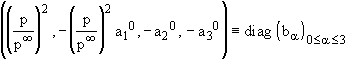, (37)

with b_i = - a_i for 1 £ i £ 3. This case includes the static case (¶p/¶t =0) and that of spherical symmetry around a fixed point in ether. The Christoffel symbols G and G ’ of the metrics g and g , respectively, have been calculated in the previous work [8b]. The first-kind symbols verify :

G '_ijk = - G_ijk (i,j,k = 1,2,3); (38)

G '_aaa = b_a,a/2, G ' _abg = 0 if a¹b¹g¹a, (39)

G '_aab = - G '_baa = g_aa,b/2 = b_a,b/2 if a¹b;

- G '_0aa = G '_aa0 = G '_a0a = b_a,0/2, G '_a0b = G '_ab0 = G ' _0ab = 0 if (a¹0 and b¹0 and a¹b), (40)

G '_00a = G '_0a0 = - G '_a00 = b_0,a /2 = p p_,a /(p^¥)² . (41)

The second-kind Christoffel’s are defined by

Since b_i = - a_i for 1 £ i £ 3, we thus have from (38):

The geodesic equation for a=0, writes in view of (40) and (42) :

and since we expect a null geodesic, this equation serves to determine the time dependence of the parameter l: y=dx⁰/dl. It comes from (41) and (42) that :

which is nil, unless if i=1. We get from (44) and (45) :

in which dp/dx⁰ is due only to the spatial variation of p along the trajectory. Eq. (46) gives

dy/y + 2 dp/p = 0 , y = dt/dl = 1/p² , (47)

in which dt/dl has been substituted for dx⁰/dl , since l may be replaced by a proportional parameter. By (43), the left-hand side of the geodesic equation writes for i=1,3 :

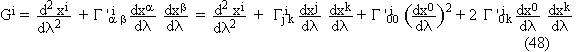
Now by (31) and (19), we write the neo-Newtonian law (30) as:

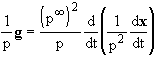, (49)

whence by (47)₂ and (18) :

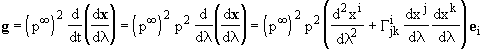, (50)

thus the two first terms in the last member of (48) represent gⁱ/[p² (p^¥)²]. From (5) and (36) :

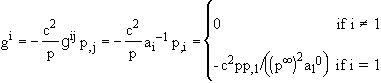(51)

Hence, by (40), the geodesic equation Gⁱ=0 is also verified for i=2,3, and the last is

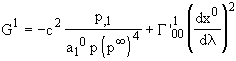. (52)

But from (37), (41), (42) and (47), we get:

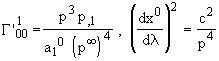. (53)

Hence the geodesic equation for photons (or other particles moving at the velocity of light) is proved independently of any field equation, from Newton's second law in the frame E. Like for ordinary particles, we assume here, by induction from this result obtained for a static field, that the geodesic motion holds true in the general case where a Newton law has not been defined.

7. SPHERICAL SYMMETRY : STATIC SOLUTION AND HYDROSTATIC EQUILIBRIUM

A spherical gravitation field has to be defined as the case where p_e or r_e depend only on the radial distance r (as measured with the Euclidean metric g⁰ making the macro-ether a rigid body M) and the time t (as measured with one clock at a given point x₀ÎM, i.e. bound to E). Then one "isopotential" coordinate system, in which the metrics g and g are given by (36) and (37), is the spherical coordinate system (r,q,f). Thus the field equation (23) writes, in view of (19) and (25) :

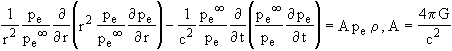, (54)

in which one may moreover assume that p_e^¥ does not depend on t, i.e. a static situation at infinity (or far enough from the massive body). Equation (54) implies that the density of mass-energy r also depends on t and r only. The static spherical solution (r_e and hence r independent of t) follows easily from (54) and was given for a general distribution r(r) with finite integral M=M(r=¥)<¥ in the previous work [8b] (no confusion can occur between the mass M and the 3D-manifold M consisting of the macro-ether):

, (55)

where M(r) = 4p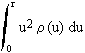; the integration constant C is non-positive, and negative only in

the unphysical case where an (1/r²)-repulsion occurs for r®0 and at the same time the field g is equivalent to GM^a/r² with M^a<M at large r. In the physical case C=0, the space-time line

element is thus, by Eq. (37) (with ):

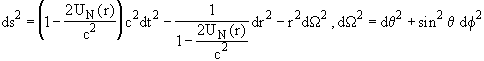(56)

and moreover the field g given by Eq. (5) (where the grad operator refers to the curved metric g), i.e. the gravity acceleration field in the sense of the modified Newton law (20) or (30), is the exact Newtonian field

g = - G M(r) e_r/r² (57)

(this is proved in [8b]). We emphasize that all of this is true for a general function r(r); in particular, if r(r)=0 for r>R, it is valid for r£R as well as for r³R. In that case, the metric (56) for r³R is the exact Schwarzschild exterior metric (U_N(r)=GM/r). However, the metric for r<R is not that predicted by GR. E.g. in the case of a uniform density, r(r)ºr₀ for r<R, the term U_N(r) in (56) is given, according to Eq. (55)₂, by

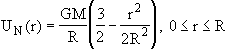, (58)

whereas Schwarzschild's interior solution is :

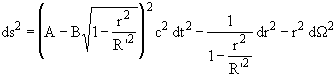, (59)

1/R' ² = 8 p G r₀ /(3c²)

with A>0 and B=1/2 (see e.g. [19]). The main difference between the interior solutions according to GR and the ETG is the following one : according to the ETG, the ratio

dl / dl⁰ = Ög_{r r} = Ö(- g_{r r} ) >1

between the radial distances as evaluated with the physical metric g and the Euclidean one g⁰ (which is equal to g at infinity) continues to increase as r goes from R to 0, whereas it decreases towards 1 for GR. The result of the ETG is in agreement with what is found from the EP, that the metric effects of gravity are given (for weak fields) by the Newtonian potential (Sect. 4), since U_N(r) in Eqs. (55),(56) and (58) turns out to be nothing else than the Newtonian potential - however, no restriction to the field strength is imposed here. Another difference with GR is that, independently of the state equation, the radius R of the body cannot be smaller than the Schwarzschild radius r_S = 2 GM/c², for otherwise Eq. (55) (with C=0, and U_N(r)=GM/r for r³R) would lead to a negative square p_e². The number R is the radius of the body as evaluated with the Euclidean metric g⁰, hence the physical radius is greater. On the other hand, the mass-energy density r is evaluated with the physical metric g , hence M= òrÖg⁰ dr dq df = òr dV⁰ is smaller than the mass of the whole energy creating the field, M' = òr dV = òrÖg dr dq df , since

Ög⁰/Ög = dV⁰ /dV = Ö(1-2 U_N(r)/c²) < 1.

The same occurs in GR, where M is interpreted as the sum of M' and the negative energy of the gravitational field [4]. A discussion of the gravitational energy in the present theory will be given elsewhere.

Since pressure does contribute to gravity in the ETG as in GR, one may expect that, as in GR, the static equilibrium is impossible if the integral M is too large : first, SR at the local scale and the definition of the energy-momentum tensor T hold true in the ETG; second, if one admits the geodesic formulation of motion in the general case (as is done in this paper), then the "conservation equation" (CE), div_gT=0, can be used in the ETG (the geodesic motion of free particles is equivalent to the CE for T with "dust" matter; the essential difference in the ETG is that geodesic motion and the CE are not a consequence of the field equation for gravity). In that case, the static equilibrium writes exactly as in GR (see e.g. Weinberg [4]). For the case of spherical symmetry, it gives using the static solution (56)-(57) :

which is not identical to the Oppenheimer-Volkoff equation. However, it may be shown that it gives the same qualitative result, i.e. the existence of a superior limit for the mass M.

8. SPHERICAL SYMMETRY : GRAVITATIONAL COLLAPSE AND GRAVITATION WAVES

From above, we take it for granted that a very massive object will necessarily undergo a dynamic transformation, either an explosion or, in the case where the (ordinary) pressure p in the body is unable to balance the gravitation force, an implosion. Since pressure increases gravity also in the ETG, we expect that, as in GR, some qualitative features of the implosion are rather resistant to the change of the unknown state equation and therefore can be found from the analysis of the oversimplified situation of dust matter. Thus, the pressure p is neglected. The particles of the collapsing body are hence free and they have a geodesic motion. Furthermore, we assume here that the body, made of freely moving dust particles, is comoving with the macro-ether (see the end of Sect. 5 : the assumption of a constitutive ether leads naturally to this hypothese for very high densities such that elementary particles are more or less contiguous to each other). We thus write in any coordinates bound to the frame E :

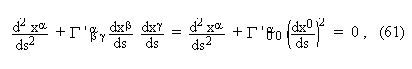
which is equivalent to

For the case of spherical symmetry around the center O of the massive body which is assumed to be comoving with ether, the spherical coordinates x¹=r, x²=q, x³=f of the Euclidean space M (the body "macro-ether"), with origin O, are indeed bound to the frame E and moreover are such that p_e does not depend on x² and x³. Thus the space-time metric is given by (37) and we get by (41) and (42) :

, ,

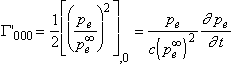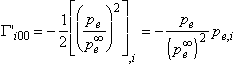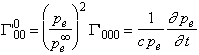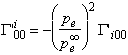, . (63)

This implies that Eq. (62)₂ is equivalent to

p_{e, i} = 0 (i = 1,...,3) , (64)

which means that the field p_e has a uniform value p_e⁰ in the massive body, occupying a domain W in the space M. This result demands that we are able to give a sense to our basic assumption (A) in a case where the direction of the field g , asked for by Eq. (16), is undetermined. We restrict the discussion of this degenerate situation to the case where the field p_e is furthermore uniform at infinity. Then, either the uniform value p_e⁰ is p_e^¥, in which case there is no space contraction in the considered domain, which must extend to infinity. Or p_e⁰ < p_e^¥, in which case the domain W, where p_eº p_e⁰ , has to be bounded. Thus, the direction of contraction is determined at the boundary ¶W, by continuity with the exterior of W where grad p_e is not nil, and the contraction ratio b=p_e/p_e^¥ has the same value at each point of W and ¶W. This may be sufficient to determine a unique direction of contraction at any point of W It is at least true in the present case of spherical symmetry, where the direction must obviously be the radial one. Now let us examine whether the condition (62)₁ gives a further requirement which should be satisfied by dust matter comoving with ether, in addition to (64). With Eqs. (63) and (64), we calculate

and

Hence (62)₁ is automatically verified if p_e depends only on t within the body.

Let the free fall begin at time t=0 : the initial distribution p_e0 must be independent of r. This is not compatible with a static situation at t=0 since, due to Eq. (55)₁ (with C=0), it would mean that the Newtonian potential U_N(r) does not depend on r inside the body - that is, for r<R - and this in turn implies that r₀(r) is nil for all r. The collapse in free fall cannot start from a static situation. The space-time metric g is given by Eq. (37) with in particular g_0i =0 (this is general in the frame E, Sect. 4). For dust matter, the mixed components of the energy-momentum tensor in the comoving frame E are therefore

and T^lm = / b² with b=p_e(t)/p_e^¥ for the contravariant ones; it follows that only the component a=0 of the CE for T is not trivially verified, and gives

We thus get :

Inserting (69) into the field equation (54) in which p_e depends only on t, we obtain :

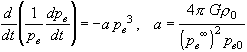, (70)

or after substitution of the proper time t, which flows uniformly in the body (dt/dt = p_e/p_e^¥):

. (71)

Note that the constancy of a and b, i.e. the fact that the initial mass-energy density r₀ actually does not depend on r, is a consequence of the field equation with a uniform field p_e(t) inside the body, but in turn, by (74), implies that r remains uniform : the collapse in free fall can occur only with a uniform material density r. We thus have already two important differences with GR.

The resolution of Eq. (71) is standard : one introduces the slope z=dp_e/dt = z(p_e) as an auxiliary function, considered as one of pe, and one writes

whence with (71) (where b=1 by changing the time unit) :

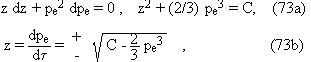
which gives t as function of p_e :

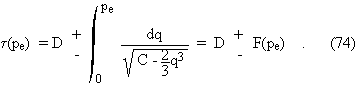
One starts with a positive value pe0 at t = t =0. The initial slope z₀ determines the integration constant C, which is positive (Eq. (73a)). In that case, if one restricts the discussion to curves which cannot go accross the (p_e=0)-axis, the solution pe to Eq. (71) is a periodic function of t , which cancels at regular intervals dt = 2 F(p_{e max}) with p_{e max} = (3C/2)^1/3 (Eq. (73a)); at those times t where p_e cancels, the slope z undergoes a discontinuity, passing from -ÖC to ÖC (Eq. (73b)). Whatever the sign of z₀ = (dp_e/dt)(t=0), the macroscopic ether pressure p_e inside the body cancels after a finite proper time. Actually, the sign of z₀ is related to the time evolution of the radius R' of the body, as evaluated with the measuring rods of the freely falling "observer" (a robust one) : assumption (A) means that R' is expressed as function of the constant radius R (as evaluated with the Euclidean metric bound with ether, as long as this remains comoving with matter) as R' = (p_e^¥ /p_e(t)) R , hence

Thus, if the local "observer" finds an implosion at t=0, one must have z₀ > 0, but then the slope z cancels at the proper time

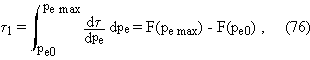
so that the sign of the time evolution of R' is changed : the implosion becomes an explosion ! moreover, as t continues to increase, p_e cancels at t₂ = t₁ + F(p_{e max}) and R'®¥ as t ® t₂ : the nil value of p_e = r_e c² means that the finite amount of ether contained in the domain r<R, and which is comoving with the body, is diluted in a domain of infinite size - as evaluated with physical rods. Once the value p_{e max} has been passed beyond, the density of matter decreases as p_e , since r=r₀ p_e/p_e0 (Eq. (69)). While r continues to decrease, say when it becomes much smaller than its initial value r₀, the argument of Sect. 5, that all ether would be involved in material particles, cannot be used any more to admit that the ether is comoving with matter (but, on the other hand, since all is uniform within the body, any reason to change this situation should have to come from an interaction with the exterior). Thus, the calculations have only an indicative value after p_e and r have gone below the values they took at the start of the free fall. During the raid in the domain of very high densities, however, the comoving of ether and matter is nearly implied by the assumption of the constitutive ether (see Sect. 5) and in turn it precludes that the collapse in free fall lead to any singularity.

The measuring rods of sufficiently far observers are not affected by gravitation (p_e » p_e^¥), thus one could be tempted to say that, as long as its density is high enough so that ether is comoving with matter, the body has a constant radius for remote observers : if the macroscopic motions of ether and matter coincide, a change in the physical size of a massive object can occur only with a change in the gravitational contraction. But as soon as the metric is influenced by gravity - and thus by such objects - it is difficult for a remote observer to define the size of an object, e.g. because the light paths become curved. By the way, can light rays escape the freely falling body in finite time t, or does it become a "black hole" ? A first point is that the time t (of far clocks) becomes infinite during the proper time t₂ (of freely falling clocks in the body or at its surface) that it takes for the value p_e inside the body to cancel, since

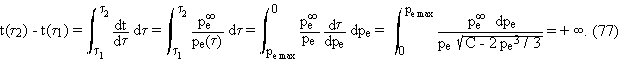
However, to answer the question about light rays, we should be able to solve the equation

which implies that we should know the field p_e(t, r). In GR, Birkhoff's theorem allows one to choose space-time coordinates in which the exterior metric is static, and thus to find ones in which it is the Schwarzschild metric. This means that, according to GR, gravitation waves cannot exist outside the massive body, in the case of spherical symmetry (see e.g. Weinberg [4]). But it is not so in the proposed theory. The field equation (54) is a hyperbolic quasi-linear differential equation in the variables (t, r), since it writes

,

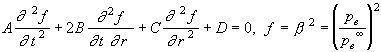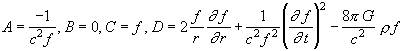. (79)

The characteristics are therefore the radial light rays :

(which shows in a demonstrative way that gravity propagates with the velocity of light in the ETG, though it is already clear from the general equation (23)). Thus, depending on the initial and boundary conditions, the solution to (79) is generally made of both outgoing and ingoing waves. In the present case, the initial condition f(t=0, r)=f₀(r) and (¶f/¶t)(t=0, r)=q₀(r) for all r ³ 0 determines uniquely the solution in the domain r £ f(t), where (r=f(t)) is the outgoing characteristic starting from the origin (t=r=0) [20], and we have seen that the initial data cannot be static, that is, q₀(r)¹0. Therefore, a non-static situation (with waves) is certainly present for t>0, and since it resolves in a uniform (but time-dependent) situation for r<R, we may confidently expect that outgoing and ingoing waves are present. Now we observe that the wave velocity w=|dr/dt|=cf=cg₀₀ decreases along the path of the ingoing wave, because the wave moves towards the direction where p_e decreases and the clocks are slowed down; we have in general :

, (81)

thus our statement is certainly true inside the body (r £ R) for t ³ t₁ (Eq. (76)), since we have then ¶f/¶r =0 and ¶f/¶t <0, whence dw/dr>0 for the ingoing wave (dr<0, e=-1); this strict inequality extends to a larger domain r < R+h(t); the inequality is also ensured at sufficiently large r, where the wave starts from a static situation. But a wave whose velocity decreases along its direction of propagation may become a shock wave if its propagation length is sufficient, as discussed by Whitham [20] (the other condition ensuring the appearance of a shock wave is that the decrease in the wave speed should be stronger than the damping of the wave; intuitively, we would say that here an ingoing wave should be reinforced rather than damped, but this must be checked). If we admit on the above basis that w decreases along ingoing characteristics in the whole domain r £ f(t) (and that ether is still comoving with matter), then we have necessarily enough time t for a shock wave to develop before the "catastrophe" p_e=0, since it takes an infinite time t [Eq. (77)] [the catastrophe relies precisely in the fact that a finite proper time corresponds to an infinite time of remote clocks (and the reverse for the spatial size), a very strange situation]. According to our theory based on a constitutive ether, a shock wave, i.e. a discontinuity in the ether pressure, should destroy the material particles made of stable local flows in ether (perhaps vortices). Thus, once a shock wave would have reached the body, an enormous amount of energy would be released, thereby ending the collapse (otherwise, the whole mass would be destroyed) and at the same time reducing the mass of the body, i.e. the cause of the collapse. Winterberg already suggested the possibility of a shock wave in gravitational collapse, within his different theory [7] (see below). This implosion-explosion cycle could repeat until the mass is small enough to allow static equilibrium. These considerations might be of interest for the interpretation of g bursts.

9. CONCLUSION

Starting from a tentative interpretation of Newtonian gravity as a pressure force in an incompressible perfect fluid or ether, one may first obtain a new theory of gravity within Newtonian mechanics, simply by giving a compressibility to the ether; this results in a finite velocity of propagation. This does not seem to have been proposed earlier, and the reason may be that one : surprisingly, the "ether pressure" p_e must decrease towards the gravitational attraction whereas the average mass density in the particles depends on p_e only and decreases with p_e, and thus also decreases towards the attraction - thus the particles would swell in the gravitation field, i.e. there, where they are closer from one another! But the density in the particles is not the density of matter (the number of particles per unit volume), hence there is no absurdity and moreover one sees then at a glance that matter cannot be indefinitely compressed (since the particles would then encroach up on one another). When one accounts for the metric effects of gravity, the essential point is the coexistence of two spatial metrics in the reference frame E of ether : an Euclidean one g⁰, which is bound to the ether (when the latter is considered at a macroscopic scale), i.e. which makes it a rigid "body"; and the physical one g, which is related to g⁰ by a contraction of measuring rods in the ratio p_e/p_e^¥ (with p_e^¥ the value of p_e in remote regions, free from gravitation), depending on time in the non-static situation. The clocks bound with E are assumed to be slowed down in the same ratio, and special relativity allows to pass to moving local frames. This assumption of gravitational contraction (resp. dilation) of space (resp. time) standards expresses the principle of equivalence between the metric effects of motion and gravitation, which has a basis in the ETG. Independently of any field equation, it allows, in the static case, to deduce the geodesic characterization of motion of ordinary as well as light-like particles from Newton's second law expressed with physical standards affected by gravitation.

The field equation for p_e obtained within Newtonian mechanics in assuming an ether compressibility keeps the same form in the modification integrating the metric effects, but it becomes non-linear in p_e. In the spherical static situation, it leads to Schwarzschild's space-time metric g outside the body, but the interior metric is different and agrees with the EP. Furthermore, the associated "acceleration" field g (Eqs. (5) and (20)) is the exact Newtonian one, inside and outside. The same interior metric as here has been found (in the particular case of uniform density) by Winterberg in his theory, also based on ether [7]. However, Winterberg's theory is very different, first in the concept of ether : he assumes that the ether is made of quantum particles, obeys (nonrelativistic) mechanics and is subjected to gravitation. Here it is continuous at any scale, the macroscopic ether of the gravitation theory defines a global inertial frame (when there is one), and gravity is caused by ether as its pressure force. Winterberg's theory needs ether plus an independent absolute space which would be a Newtonian inertial frame for the moving ether (Winterberg's ether has a macroscopic motion even in the static case). Winterberg's field equation also is very different, since it is one for a 4-vector potential (instead of scalar here) and it is linear in this potential, very much like the equations for the electromagnetic vector and scalar potentials.

The basic assumption that the material particles are local flows in the fluid ether [13] leads to admit that, in the case of very high density, the macroscopic motions of ether and matter coincide. The study of gravitational collapse in free fall (CFF) with spherical symmetry, made under this assumption, exhibits marked differences with GR. If nothing would stop the free "fall", the implosion would necessarily be followed by an explosion in such a way that, as seen from local observers, the space within the body would become infinite. This is the exact contrary of the point singularity of GR; perhaps our calculation is less justifiable when the density ceases to be very high, but it does apply to preclude the occurrence of a singularity with infinite density. Moreover, according to the proposed theory, gravitation waves (moving at the velocity of light) may well exist outside a body also in the case of spherical symmetry, and indeed in the situation of CFF the occurrence of an ingoing shock wave seems quite plausible, which would release energy and stop the free fall.

It is emphasized that the present theory is non-covariant; this is logically consistent since it assumes a privileged frame. But therefore, the fact that Schwarzschild's exterior metric is found in the static case with spherical symmetry does not completely assure that such observational data as the advance in the perihelion of planetary orbits are satisfactorily predicted : it is necessary to build an equivalent of the post-Newtonian (pN) approximation of GR and to check that it agrees with observational data. Progress is currently being made in this direction and the results obtained so far seem to remain compatible with this requirement, although a further investigation is still needed. In particular, this research in progress has already shown that no gravitation wave can be found in the first pN correction. The pN approximation also shows that the theory with Newtonian space and time (Sect. 2) is not a consistent approximation of the present theory, since the effects of the compressibility cannot be separated from the metric effects.

A recent result is that a consistent Newton law can also be defined in the general (time-dependent) situation, and leads to a true conservation equation for the energy; this includes both the (negative) potential energy of matter in the gravitation field and the positive energy of the gravitation field itself. However, the Newton law is not compatible with geodesic motion in time-dependent situations. The energy conservation equation, together with the weak-field, linear approximation of the present theory, allow to calculate the gravitational radiation flux in a way similar to that followed in linearized GR. In particular, if the center of mass of the gravitating system is at rest in the privileged frame or "ether", this radiation flux corresponds to an energy loss which depends only on the third time derivative of the quadrupole tensor and involves a G/c⁵ factor (this is much as the famous "quadrupole formulae" of GR, on which are based the estimates of the secular decrease in the orbital period for a binary system). For this question also, however, it remains to verify that the effect of changing the reference frame is small for expectable absolute velocities.

Let us finally comment on the Lense-Thirring effect: this is a prediction of GR, according to which the rotation of a massive body should manifest itself by a "magnetic" component of the gravitation field, thereby causing a specific precession of the orbit of any test particle around the body. This effect comes from the fact that in GR: (i) particles move along geodesics and (ii) non-zero g_0i components of metric g are predicted in the case of stationary rotation [4,18]. In the present theory, a stationary rotation of a massive body, with respect to the privileged frame E, causes a constant field of "ether pressure" p_e and, in that case, this theory also predicts geodesic motion of test particles- but the g_0i components are always zero in the frame E. This frame is inertial in the sense that the Newton law is written in E, and for constant field p_e it is rigid with respect to the physical space metric, in short it is an inertial frame in the astronomical sense. Hence, the Lense-Thirring effect does not exist according to the present theory. But the frame E is defined by the average motion of the assumed microscopic constitutive ether. Therefore, the rotation of the massive body, as any motion of matter, contributes to the motion of the frame E, by a simple weighting effect. This means that the theory is in agreement with Mach's principle, because the preferred inertial frame (playing the role of Newton's absolute space, and indeed exactly the same role in the limit of weak and slowly varying fields) is influenced by all motions of material bodies.

ACKNOWLEDGEMENTS

I am very grateful to Prof. P. Guélin for many helpful discussions and comments on this work. It is also a pleasure to thank Prof. E. Soos for his interesting remarks on this subject. The interest of the questions of a referee, on the gravitational radiation and the Lense-Thirring effect, is also acknowledged.

Received June 26, 1995

REFERENCES

[1] A. Papapetrou, Proc. Phys. Soc. A64, 57 (1951).

[2] V. Fock, The theory of space, time and gravitation, Pergamon, Oxford 1964.

[3] T. Damour and N. Deruelle, Ann. Inst. Henri Poincaré (Phys. Th.) 43 (1), 107 (1985).

[4] S. Weinberg, Gravitation and cosmology, J. Wiley & Sons, New York 1972.

[5] A. A. Logunov, Yu. M. Loskutov and M. A. Mestvirishvili, Sov. Phys. Usp. 31 (7), 581 (1988) (Transl. from Uspekhi Fiz. Nauk 155, 369 (1988)).

[6] D. W. Sciama, in "The philosophy of vacuum" (S. Saunders & H.R. Brown, eds.), Clarendon Press, Oxford 1991, p. 137.

[7] F. Winterberg, Z. Naturforsch. 43a, 369 (1988).

[8] M. Arminjon, Rev. Roum. Sci. Techn.- Méc. Appl. 38, (a) 3 and (b) 107 (1993).

[9] L. Euler, Opera omnia, Ser. 3, i: Commentationes physicae, pp. 3-15 and pp.149-156 (1746).

[10] G. Builder, Austr. J. Phys. 11, (a) 279 and (b) 457 (1958).

[11] S. J. Prokhovnik, The Logic of special Relativity, Cambridge University Press, Cambridge 1967.

[12] A. Einstein, Sidelights on Relativity, Methuen, London 1922.

[13] L. Romani, Théorie générale de l'univers physique (réduction à la cinématique), Blanchard, Paris 1975 (vol. 1) and Paris 1976 (vol. 2).

[14] A. Einstein, Ann. d. Phys. 38, 355 (1912).

[15] E. Soós, Rev. Roum. Sci. Techn.- Méc. Appl. 37, (a) 127 and (b) 245 (1992).

[16] J. L. Synge, Relativity, the general theory, North-Holland, Amsterdam 1964.

[17] M. v. Laue, Phys. Z. 21, 659 (1920).

[18] L. Landau, E. Lifchitz, Théorie des champs, Mir, Moscow 1970.

[19] S. Mavridès, L'univers relativiste, Masson, Paris 1973.

[20] G.B. Whitham, Linear and non-linear waves, J. Wiley & Sons, New York 1974.

To the beginning of “Scalar theory of gravity as a pressure force”

To the top of this page (Section 6 of “Scalar theory…”)