Scalar theory of gravity as a pressure force
Revue
Roumaine des Sciences Techniques - Mécanique Appliquée, 42, No. 1-2, pp. 27-57 (1997)
Mayeul
Arminjon
Laboratoire "Sols, Solides,
Structures",
Institut de Mécanique de Grenoble, France.
Warning: Depending on the navigator, the characters (Times) g, used for
the gravity acceleration vector, and (Arial) g, used for the spatial metric, may appear in the same font. Also, the
square (d’Alembert operator) may not appear at all. I have a
few offprints. M.A. (mailto:arminjon@hmg.inpg.fr)
Abstract- The construction of this theory starts with Newtonian space-time and a
tentative interpretation of gravity as Archimedes' thrust exerted on matter at
the scale of elementary particles by an imagined perfect fluid or ether. This
leads to express the gravity acceleration by a simple formula in which the
"ether pressure" pe plays
the role of the Newtonian potential. The instantaneous propagation of Newtonian
gravity is obtained with an incompressible ether, giving a field equation for pe. For a compressible ether, this equation holds in the
static case and results in a non-linear influence of the mass distribution. The
extension of the field equation to non-static situations follows the lines of
acoustics and leads to gravitational (pressure) waves. To account for metric
effects, first the modern version of the Lorentz-Poincaré interpretation of
special relativity is summarized. Then Einstein's equivalence principle (EP) is
seen as a correspondence between the metric effects of gravity and those of
uniform motion with respect to the ether : a gravitational contraction
(dilation) of space (time) standards is assumed, and it implies geodesic motion
for test particles in a static field. The same field equation is now expressed
in terms of the physical space and time metrics in the frame of ether; since
both metrics depend on pe due to
the EP, it becomes non-linear in pe. In the spherical static situation, Schwarzschild's exterior metric is
predicted, but the interior metric differs from GR, though it agrees with the EP.
Since pressure produces gravitation also in the proposed theory, no equilibrium
is possible for very massive objects. But the gravitational collapse in free
fall does not lead to any singularity. Moreover, gravitational waves, and even
shock ones, can exist in vacuo also
with spherical symmetry.
Keywords: Gravitation,
Ether, Relativity, Relativistic Dynamics, Gravitational Collapse.
Postal address: Laboratoire
"Sols, Solides, Structures", E.N.S.H.M.G., BP 53, 38041 Grenoble cedex 9, France.
1. INTRODUCTION
Of the reasons that may
justify the search for alternatives to general relativity (GR), some are
comparatively recent : the complete implosion into a point singularity, which
is predicted for very massive objects and which could not be detected in the
case of spherical symmetry; the isolation of gravitation with respect to the
theories of other interactions (this expressed earlier in the problem of
unifying gravitation with electromagnetism, and more recently in the difficulties
with quantum gravity); and, finally, the problems of interpretation which are
due to the need for a non-covariant coordinate condition : Papapetrou [1]
already suggested that different coordinate conditions might lead to different
post-Newtonian equations of motion, and Fock [2] observed (at § 96) that
indeed, the coordinates used by Einstein and Infeld differed from harmonic
coordinates, used by Fock and Papapetrou, only by second-order (O(1/c4)) terms which play no role in the first corrections
to Newton's theory; today the post-Newtonian calculations are very generally
formulated in terms of harmonic coordinates [3, 4]. According to Logunov et al. [5], one has to modify GR into a
"relativistic theory of gravitation" such that, essentially, Fock's harmonic
condition is organically contained in the new theory, for otherwise GR would
not furnish unique predictions. Thus the general covariance is not a sine qua non condition; in this paper, a
theory with a privileged frame is investigated. In the writer's opinion, the
most fundamental question that remains unsolved by GR was already posed to
Newton's theory : how can interactions propagate through empty space ? Why not
try to give physical properties to empty space, in such a way that the
propagation of gravity as well as the existence of global inertial frames (i.e. as they appear in Newtonian theory)
become understandable? The existence of
the zero-point fluctuations makes it necessary to admit that vacuum indeed has physical properties
[6,7]. A comparison of Winterberg's ether theory of gravitation [7] with the
one proposed here, which will be designated by ETG for short, is deferred to
the Conclusion for convenience.
Already within the
Newtonian concept of absolute space and time, gravity can be tentatively
interpreted as Archimedes's thrust, due to the pressure of an hypothetical,
perfect fluid or ether, surrounding all elementary particles of matter : the
condition of validity is that all particles should have the same mass density -
or at least that their average density depends only on the pressure in the
fluid [8a]. It turns out that Newtonian gravity (NG) was first interpreted in
this way a long time ago by Euler [9]. Under the condition that NG must be
recovered for an incompressible fluid, a (scalar) field equation is obtained
for the ether pressure; after a compressibility is introduced, this
"ETG" gives qualitatively correct modifications to NG : a finite wave
speed and an advance in the perihelion of planetary orbits which is proportional
to the prediction of GR [8a]. To go further, it is necessary to have a
description of the relativistic effects. The first step is to realize that the
old Lorentz-Poincaré ether interpretation of special relativity can be updated
with the same logical thrift and consistency that have made Einstein's theory
so convincing [10,11]. The "new" ether interpretation reconciles
Lorentz's original view of a true contraction in the absolute motion with
respect to the ether, with the reciprocity of the Lorentz transformation in the
version found by Einstein; it will be once more summarized in this paper. The
possibility of this interpretation and its great interest were recognized by
Einstein [12] himself (see Builder [10a]). Hereafter, the transition is made to
the gravitational situation in which the ether pressure (or equivalently the
ether density, since the ether postulated here is a barotropic perfect fluid)
varies from one point to another - which is the cause of gravity in the
proposed ETG. Special relativity holds then only locally, i.e. in a domain
where the ether density may be considered uniform. The true Lorentz
space-contraction and time-dilation with motion lead naturally to a new
formulation of Einstein's equivalence principle, within the ETG : gravitational
space-contraction and time-dilation are postulated; with this assumption and
when the proposed equation for the field of ether pressure is reinterpreted as
relative to the physical, distorted space and time standards, Schwarzschild's
exterior space-time metric is exactly recovered in the static situation with
spherical symmetry [8b]. Moreover, for any static gravitation field, the
geodesic characterization of the motion of free mass points follows from this
assumption and Newton's second law (with the momentum including the
velocity-dependent mass and all being measured with the local clock and
measuring rod), independently of the field equation.
In this paper, a
synthetic presentation of this scalar theory of gravitation is given. Several
new results are reported : a discussion of the Newtonian limit; an extension to
light-like particles of the proof that Newton's second law (interpreted as
above) implies geodesic trajectories; a brief study of gravitational collapse
and gravitational waves with spherical symmetry. For these two last problems,
the situation in this theory differs strongly from that in GR.
2. THE ETHER THEORY OF GRAVITATION WITHIN NEWTONIAN MECHANICS
Following physicists of
the past like Euler, Helmholtz and Kelvin, it is found that only a perfect
fluid, i.e. without viscosity, could fill the space left by matter without
braking any motion : this is well-known in fluid mechanics as d'Alembert's
paradox. Such a fluid acts only by its pressure pe; it
would exert over a material domain W , the force
F = ò¶W -pe n dS
= - òW grad pe dV (1)
(¶W is the
boundary of W, n is the outward normal, S
and V are the surface and volume measures). We want that F is the gravitation force :
F = òW r g dV , (2)
with g the gravity
acceleration and r the mass density. If we think of W as being a
macroscopic domain where g may be
considered uniform (and for the real gravity this is true even with rather
large domains), this equality cannot hold, since g in (2) and grad pe in (1) should not depend on the
kind and state of matter in W, while r of course does. However, the macroscopic matter is
made of particles which are already subjected to the gravitation, hence the
fluid pressure would have to act only on a small part of the macroscopic volume
W : the union of the volumes wi (i=1,N(W)) occupied by
the constitutive particles. In other words, the fluid would fill the place left
by the particles. Let ri be the
mass density of particle (i). In order that (1) and (2) coincide when W=wi and r=ri, it is necessary that ri be independent of the particle (i), and then the
pressure force (1) would also be a mass force (2) for a macroscopic domain W, provided
that grad pe also be
uniform in W :
F = - grad pe S V(wi ) = g S mi = g S ri V(wi ) . (3)
Thus, we come to the conclusion that one should have :
g = - grad pe /rp
, (4)
with rp the
assumed common density of the particles - which could still depend on the pressure
pe in the thought ether. Now the identity between
inertial and passive gravitational mass does not seem to be known with the same
precision for elementary particles than for macroscopic matter. The density in
the particles might thus be allowed to vary from one particle to another, so we
take for rp the average mass density in the different
particles of a macroscopic domain W : rp= S riV(wi)/ S V(wi). But in
order that g in (4) does not depend
on the kind of present matter, rp must be a
function of the state parameters of the ether alone. Since the ether is assumed
to be perfectly continuous at any scale, no temperature and no entropy can be
defined for it, so the state parameters reduce to the pressure pe and the
"mass" density re which
are related together by the barotropic state equation [13]; hence rp must depend only on pe. This
seems to be possible only if the particles of matter are themselves ether :
from the attempt to describe gravity as a pressure force in a fluid ether, we
are lead to the assumption of a constitutive
ether, which was a priori set by Romani [13].
Assuming therefore that re = rp , we obtain the gravity acceleration
as
![]()
but this equation may be taken as a phenomenological
equation for g (alternative to
the Newtonian equation g = grad U ;
note that in Newtonian theory, the potential U, as here the pressure pe of the
imagined fluid, manifests itself only through g). The foregoing microscopic considerations are then a heuristic
justification for Eq. (5). We note that pe and re should be the macroscopic pressure and density in the thought ether, since the
gravitation varies only over macroscopic distances and due to the effect of
macroscopic bodies. This remark is important in the context of a possible
unification of the four known physical interactions within a theory of this
barotropic ether : the other interactions, which vary over shorter distances,
would then have to be all contained in the microscopic fluctuations of ether
pressure and velocity. In fact, Romani [13] described a way in which this may
be done, in assuming that all known particles would be vortex tori or complexes
of such flows; he proposed to explain the appearance of quantum numbers from
the requirement that the helicoidal trajectories on the torus should be closed.
Yet his work, while very interesting, suffers in some places from a lack of
rigour, and contains no field equation. Furthermore, gravity was the least
developed part of his work and if he attributed this force to a gradient of
ether density in the barotropic ether [13, vol. 1], he stated that the
deviation of light rays passing near the Sun should be due to an increase of
this density towards the Sun [13, vol. 2] - whereas it follows immediately from
our Eq. (5) that pe and re decrease
towards the gravitational attraction. In
the present work, our aim is to deduce from the assumption of the barotropic
constitutive ether a phenomenological theory for gravity, in a classical
framework, i.e. without trying to obtain a quantized gravity, and also without
any claim of describing the other interactions. Inasmuch as a theory of
gravity has to be compared with NG and GR which are also phenomenological
theories, we thus do not care about the fact that, of course, quantum mechanics
would scarcely allow to define a mass density for an elementary particle, and
would not allow to use classical mechanics at this level : within the Newtonian
space-time, the theory describes gravity by a potential (Eq. (17a) below) which
might be used as a phenomenological description of this interaction, also at
the quantum level, in non-relativistic quantum mechanics. Also, once modified
to account for "relativistic" effects, the investigated theory, just
like GR, will finally lead to a curved space-time, the curvature being bound to
the distribution of matter; this is in turn adapted to describe gravity in
relativistic quantum mechanics.
In this phenomenological view,
the next step is to recover Newtonian gravity. This is a straightforward task,
for NG propagates with infinite velocity and thus must correspond to the
incompressible case; with a uniform re , we get
from Eq. (5) by using Poisson's equation (div g = -4 p G r with G Newton's gravitation constant) :
Dpe = 4p G r re
. (6)
With a uniform re , Eqs. (5)
and (6) give exactly the same description of the field g as the usual equations DU = -4 p G r and g =
grad U. The point is that (5) and (6), together with the barotropic equation re = re(pe) (of which the incompressible case
is a degenerate one), make sense as well if the ether is compressible (i.e.
when re is an
increasing function of pe). In that case, however, we have a
new, non-linear field equation for gravity : the fields pe and g depend non-linearly of the matter
distribution r, even if the pe-re relationship is linear. The static case with
spherical symmetry has been investigated analytically : one obtains a complete
solution that tends towards the Newtonian one as the compressibility tends
towards zero, and the exterior solution gives an advance in the perihelion of
elliptic orbits which is proportional to the prediction of GR [8a]; in ref.
[8a], an extension of Newtonian mechanics to fluid inertial frames is also proposed, consistently with the
assumption that the frame bound to the macroscopic motion of the fluid ether
(the "macro-ether") defines an inertial frame. In the case where the
relationship is assumed to be pe=rec2 with c
the velocity of light (as we will be lead to, Sect. 4), Eq. (6) writes
Dpe = (4p G/c2) r pe
(6bis)
which is formally identical to a relativistic equation proposed for
static situations by Einstein [14] before he finally came to GR; yet in Einstein's
equation the field was of course not pe but
instead the velocity of light w, as expressed in terms of a
"universal" time coordinate [this circumstance was not known to the
writer for the work [8]; the writer learned this in the papers by Soós [15], who presents a systematic analysis of Kepler's
problem in Einstein's successive theories of gravitation].
A motion of massive bodies
causes a disturbance in the gravitation field, i.e. in the field of ether
pressure pe; but with a compressible ether, this disturbance in
the field pe cannot propagate instantaneously and instead should
propagate as a pressure wave. A non-static situation is thus obtained. On
assuming that : (i) the ether is conserved; (ii) the disturbed motion of the
ether, i.e. its motion with respect to
the "macro-ether" which defines the inertial frame, obeys
Newton's second law; (iii) the disturbance in the fields (pe1 for
ether pressure and ve1 for ether velocity) is small, the latter being
assessed with respect to the "sound" velocity
![]()
and (iv) the undisturbed fields pe0 and re0 of a local decomposition
pe=pe0 + pe1 , pe1 << pe0
and ¶pe0/¶t << ¶pe1/¶t (7bis)
obey Eq. (6), it has been proved in [8a] that the general, non-static situation
is governed by the equation :
Dpe ![]() = 4p G r re .
(8)
= 4p G r re .
(8)
Equation (8) clearly admits pressure waves, i.e. gravitational waves propagating at the velocity ce(re).
The "macro-ether" is a primary concept
in the proposed theory. With respect to an arbitrary reference frame R, the velocity ve0 of the macro-ether is related to that of the microscopic ether (that
which is thought to be concerned with particles and shorter-range fields) by an
averaging over domains W such that the ether pressure is uniform in W (but varies
over larger scales).
3. SPECIAL RELATIVITY AND ETHER THEORY
It is well-known that Lorentz
and Poincaré, whose analyses were dependent on the assumption of the rigid luminiferous ether, derived some
basic results (formulae) of special relativity (SR) before Einstein who's
starting point was the relativity
principle. Our point here is not to raise a discussion on the extent to
which Lorentz and Poincaré did open SR : it is only to briefly recall why the
whole of SR, in its usual formulation due to Einstein, can be consistently
derived from the above ether assumption; this has been established by several
physicists among which Builder [10] and Prokhovnik [11]. The crucial step is to
recover the usual Lorentz transformation from the mere assumption (Fitzgerald
and Lorentz) of an absolute contraction of all material objects when carried
over from the rest frame E of the ether to a frame Eu that
moves with uniform and constant velocity u
with respect to E. The contraction occurs on lines parallel to u, but not on perpendicular lines. Its
ratio b(u) depends only on the modulus u=|u|
(this results from the assumed isotropy of electromagnetic interaction in the
frame E), in a way that
does not need to be assumed in advance [8b]. Let l be the length of a rod AB, when it was at rest in E, and l' its length, evaluated from E, when this
same rod is now at rest in Eu and
makes, for E, the angle q with u.
The assumed contraction implies that
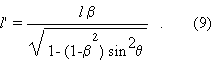
Consider AB (with a mirror at A perpendicular to AB and the like at B)
as a "light clock", its time unit being the interval during which the
light goes from A to B back and forth. To calculate the time unit Dtu(q), for E, of this light clock as it is now in Eu, we need only space and time measurements in E, so we can
write if a light wave front going from A to B intersects the rod at M (and the
point O being bound to E):
![]()
whence c1 = ![]() - u cos q and similarly c2 =
- u cos q and similarly c2 = ![]() + u cos q in the BA
direction. Therefore,
+ u cos q in the BA
direction. Therefore,
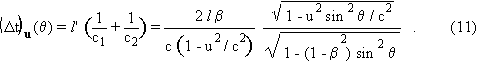
The "negative" Michelson-Morley experiment means exactly that
this period does not depend on angle q and thus is a constant in the moving frame Eu. From (11), we see that this is true if and only if
one has
![]()
The negative Michelson experiment means that light
clocks are correct clocks, and this implies the Lorentz contraction. Moreover, the
time unit of Eu is "dilated" : (Dt)u = Dt/b. Prokhovnik shows precisely that these results, together with the
standard synchronization of clocks, imply the kinematics of SR in Einstein's
form, i.e. imply first the constancy of c (as this is measured with clocks and rods
of any frame in uniform motion Eu) and
then the usual Lorentz transformation [11]. The difference with the usual
version is in the perfectly clear interpretation of the space contraction and
time dilation as absolute effects. The relativity of simultaneity is
interpreted as an artefact due to the necessity of synchronizing clocks with
light signals and to the anisotropic "true" propagation of light, Eq.
(10), in a frame that moves with respect to the propagating medium E. The true
simultaneity is defined with the time of E, and could take an operational significance if the
velocity with respect to E could be known.
Then, the dynamics of SR
follow essentially from its kinematics and from the requirement to save
Newton's second law in E as well as at least a weak form of the principle of
inertia (WPI) - namely that the momentum conservation for an isolated system of
mass points pass from E to Eu [8b,11].
One realizes first that this can be true only if the inertial mass depends on
the relative velocity, m=m(v). On assuming that the m(v) dependence is the same
in E and in Eu , the WPI
leads to the expression of m(v) and the kinetic energy T in SR :
m(v) = m(v=0)/b(v) , T =
(m(v)-m(0)) c2
. (13)
Einstein's form of Newton's second law is thus obtained in E :
![]()
and the requirement that it is Lorentz-covariant, i.e. holds true when
passing from E to Eu ,
determines the transformation of F.
The momentum conservation can be postulated also in the case of non-conserved
rest masses (i.e. creation/annihilation processes), and this extension also
passes from E to Eu if and
only if the total mass is conserved :
![]() . (15)
. (15)
Together with Eq. (13)2, this gives
the classical argument of SR for attributing to any particle the "rest
energy" m(0)c2 and
identifying mass and energy, up to the factor c2.
4. EQUIVALENCE PRINCIPLE AND ETHER THEORY
As shown by Fock [2] and
Synge [16], Einstein's equivalence principle (EP) between effects of a
gravitational field and inertial effects has to be used with some care; in
particular, it is only valid in the infinitesimal, i.e. for uniform fields. Yet
in a relativistic theory, the unifor-mity must be in space-time (i.e. the
infinitesimal domain to consider is in space-time), thus the local equivalence
should already apply with a uniform and non-accelerated
motion. Hence a such motion should have "inertial" or
pseudo-gravitational effects. This is readily verified, for in GR gravity
manifests itself by effects on clocks and rods, and effects of this kind are
indeed predicted by SR for non-accelerated motion; and again because the
equivalence is for uniform fields, the metric effects of non-accelerated motion
should be the essential ones when looking for the metric effects of gravity.
This is apparent in Einstein's rotating disc. In this example, the metric
effects are indeed assumed to depend on the local velocity, v = rw (w is the constant spin rate of the disc with respect to
the inertial reference frame). Moreover, the pseudo-gravitational
(acceleration) field has intensity a
= rw2 er = grad (v2/2); since the radial distance r is not fixed, the metric effects are
bound in no way to the local intensity of the field, but instead to its
potential (the same conclusion is drawn if one considers an accelerated
translation). Thus, an analysis based on EP indicates unambiguously that the
effects of gravitation on the space-time metric : (i) are bound to the gravity
potential rather than to the field intensity, and (ii) should be deduced from
the effects of non-accelerated motion. In the orthodox relativistic view, the
second conclusion is difficult to accept, because no inertial frame is
privileged there and the metric effects of non-accelerated motion are hence a
kind of "parallax in space-time" rather than absolute ones, whereas
the presence of a gravitational field is surely something "absolute",
that cannot be removed by changing the reference frame - except, and for one
part only, in the infinitesimal. The EP together with Einstein's lift and disc
are often used in GR to introduce Einstein's idea that gravitation is (nothing else than) a curved
space-time metric with (1,3) signature, the geodesic lines of which are the
trajectories of free test particles. However, Einstein's field equations cannot
be obtained directly as a modification of Newton's accounting for EP, and this
might be related to the above-mentioned difficulty with the absolute effects of
uniform motion.
In a theory
based on ether, there is no logical difficulty in assigning absolute effects to
uniform motion with respect to the ether. Furthermore, there is in the proposed
ETG a basis for the EP when this is seen as a relationship between the metric
effects of motion (depending only on the velocity, i.e. on the locally tangent
uniform motion) and those of gravitation. Gravitation is for us a variation in
the ether density re , and a
variation in the apparent ether density indeed occurs in uniform motion, due to
the Lorentz contraction : for an observer having a constant velocity u with respect to E, a given
volume dV0 of ether has a greater volume dV=dV0/b(u), because his measuring rod is contracted in the
ratio b in the direction u. The
"mass" or rather the amount of ether is unchanged, for the mass
increase with velocity concerns only material particles : the "mass"
of the macro-ether is not a mass in the mechanical sense [8a]. Thus the
apparent ether density is lowered, reu = re.b(u). This way of
reasoning assumes that the moving observer can use the "true"
simultaneity (of the frame E), which is true if he knows his velocity u; with the simultaneity defined from
clock synchronization in the frame Eu, the
apparent ether density would be r'eu = re/b(u) since
dV'=dV0.b(u) as deduced from standard Lorentz
transformation. In any case, the metric effects of uniform motion are given by
the ratio of an apparent ether density to that of the reference ether density, b(u)=reu/re = re/r'eu <1. It is therefore natural to postulate that :
(A) In a
gravitation field, material objects are contracted, only in the direction of
the field g=-grad pe/re , in the ratio
bg = re / re¥ < 1 , (16)
where re¥ is the ether density
at a point where no gravity is present, and the clock periods are dilated in
the same ratio.
This statement is made for
objects and clocks bound with E; if this is not so, one has to combine the metric
effects due to motion and gravitation. Due to the space-contraction of
measuring rods in the direction g,
the physical space metric g in the frame E becomes a Riemannian one. The contraction occurs with
respect to an abstract Euclidean metric, which we assume that the macro-ether
may be equipped with, as a 3-D manifold M : we assume that M is diffeomorphic
to R3 ; let us precise that M is the same
manifold at any time, since the body "macro-ether" (Sect. 2) is
followed from its own rest frame. However, an infinity of different flat
metrics may be defined on a such manifold [1]. It is thus more exact to formulate the above
assumption in stating : that space
metric g0 (in the frame E) which is (uniquely) deduced from the physical one g by the
dilation of length standards in the ratio re¥/re >1 in
the direction g , is a flat metric [2]. Therefore, the value re¥ does not need to be reached : it is the unique value
for which the assumption holds. There are three further arguments for
assumption (A) :
(i) according to the ETG, the
gravity acceleration g derives from the potential :
U = -ce2 Log(re/re¥),
(17a)
with = ce(re) (this
is deduced from Eq. (5) after linearization of the pe - re
relationship around re¥ and holds thus
either for a weak field or if the pe - re
relationship is linear); for a weak field:
U » ce2 (re¥ - re)/ re¥ , 1 - U/ce2 » re / re¥ (17b)
Furthermore, in the theory of the fluid constitutive ether, the material
particles are local flows in ether (vortex tori, or complexes of such flows)
and therefore their speed is limited by the local "sound" velocity ce [13].
Since SR gives the other limit c, one
must have ce º c, which
implies that the pe-re relationship
is in fact linear, pe = c2 re . Now it is well-known that the EP
implies that in a weak field any clock is slowed down in the ratio b = 1 - U/c2 (this
follows immediately from Einstein's analysis of the disc or lift, cf. supra),
hence the EP together with Eq. (17) give Eq. (16) for weak fields.
(ii) It is easy to check that if
one states assumption (A) without giving the ratio bg by Eq.
(16), this latter (possibly combined with the a(t) factor, see above) is equivalent
to say that, as evaluated with respect to the Euclidean metric g0, the
ether density is uniform (in space). Since this metric is by hypothese bound to
the ether, i.e. makes the ether a rigid body, it is only natural that it
renders the ether density uniform and thus the unknown ratio bg must be
given by Eq. (16). This result also confirms, if there could be any doubt, that
in the modification of the ETG accounting for SR and EP, the equations will
have to be understood as relative to the physical metric g instead of the
abstract metric g0 , for the ETG assumes an ether compressibility K¹0 (and now Kº1/c2).
(iii) Let us investigate whether
the ETG leaves the possibility of a Newton law in the frame E, in the
presence of gravitation and Riemannian space-time (as already seen, the space
and time standards must be the local, physical ones). The time-derivative of a
vector (the momentum) may be consistently defined as a vector in the case of
the Riemannian metric g on the manifold M, if g is time-independent [8b]. If P (e.g. the momentum of a mass point) is a vector attached to a
moving point whose position x in M
depends on the arbitrary time-coordinate t, one defines then its derivative
(relative to this coordinate t) by
![]()
with vk = dxk/dt and the G's being the Christoffel symbols associated with the
metric g=(gij) in the
considered coordinate system (xk); this
defines a true vector (the components (18) are contravariant with respect to
any transformation of space
coordinates). Thus an exact Newton law can be defined if re and hence g do not depend
on time. The expression of the momentum is known from SR, P=m(u)u, the velocity u and its modulus u being defined with
clocks and rods of the momentarily coincident point of M : uk=dxk/dtx=vk dt/dtx , tx being the local time defined by assumption (A) : if
t=tx0 is the proper time of a fixed point x0ÎM, one gets in
general from Eq. (16) :
dt/dtx = dtx0/dtx = re(x0,t)/re(x,t) = re0/re , (19)
though in the present case re does not
depend on t. The gravitation force involves the gravity acceleration g (Eq. (5) where the gradient is
defined with g) and the passive gravitational mass mp. According to the EP, in its weak form already true
in Newtonian theory, mp equals
the inertial mass, here m(u). Thus our modified Newton law writes :
![]()
where F0 is the
non-gravitational force and the time derivative of the momentum is calculated
with Eq. (18); equation (20) is invariant under the change of the reference point
bound with ether, x0. Now we have the following result [8b] :
(G) if the gravitation field is
constant in the frame E, then the
solution trajectories of the modified Newton law with purely gravitational
force, Eq. (20) with F0=0, are geodesic lines of the space-time metric deduced by assumption (A);
the line element of this metric g writes in the
frame E :
ds2 = c2 dt2 = (re/re0)2 (dx0)2 - dl2 , (21)
where t is the proper time of the test particle, x0=ct (t=tx0) and dl2 is the space line element calculated with the space
metric g in the frame E :
dl2 = u2 dtx2
, u2 = g(u,u) = gij ui uj . (22)
Thus, the modified Newton
law (20), which is not even Lorentz-covariant, implies the geodesic
characterization of motion which is generally covariant. We assume here, by
induction from the result (G), that free test particles also follow the
geodesic lines of g if re and g are
time-dependent, in which case we have not defined a Newton law. However, if the
time variation of re is small in such a way that the corresponding terms
are negligible in the equation of space-time geodesics (or more generally in
the expression of the four-acceleration of any test particle, "free or
not"), then an approximate Newton law (20) is obtained by still using the
definition (18) for the derivative of the momentum. Note that, due to Eq. (21),
the components g0i (i=1,3) of g are always nil in the frame E. In particular, a constant
(time-independent) re corresponds to what is called a static field in GR.
5. FIELD EQUATION, NEWTONIAN LIMIT AND INERTIAL FRAMES
The result (G) does not
depend on the field equation. To adapt this latter to the situation where the
metric modifications due to motion and gravitation are accounted, we first note
that, in the static case, the whole of the arguments in Sect. 2 may be repeated
to obtain Eqs. (5) and (6), but this time with the Riemannian space metric g (the
requirement that Newtonian theory must be recovered for an incompressible ether
remains as it stands since, from Eq. (16), the Euclidean metric is regained
simultaneously with Poisson's equation as the compressibility tends towards
zero). In the non-static case, the reasonment, detailed in [8a] and based on
the assumptions (i) to (iv) in Sect. 2 here, is not so easy to modify in a
clear-cut way, in so far as we have no Newton law any more. However, the same
equation (8) should be obtained in terms of the physical space and time metrics
in the frame E :
Dg pe ![]() = 4p G r re .
(23)
= 4p G r re .
(23)
Indeed, the proposed approach leads unambiguously to this equation in
the static case, and Eq.(23) is merely the natural expression of Eq. (8) once
it has been recognized that the non-uniform physical
space and time metrics are relevant. Thus one is strongly inclined to assume
Eq. (23) - and so we do. We emphasize, however, that in (23) the Laplace
operator D is defined with the physical space metric g which is curved and whose expression in terms of the
Euclidean metric g0 bound to
M, depends on the unknown pe through assumption (A); in the same way, the local
time tx depends
on pe or re (Eq. (19)). Hence the left-hand side
of Eq.(23) is not that of d'Alembert's classical wave equation and instead
depends non-linearly on pe . It is also worth to note that the
operator on the left of Eq. (23), which is linear if g or pe is
considered given, but which is here precisely applied to pe , is not even the modified d'Alembert or operator of GR, which is defined from the Riemannian
space-time metric g by
f = divg (gradg f) = (1/Ö|g|) (¶/¶xa)(Ö|g| gab ¶f/¶xb)
, (24)
with g = det (gab). In fact, the Laplace operator in (23) is defined from the same
formula by substituting the space metric g for the space-time metric g , and thus with summation on latine indices i and j (from 1 to 3)
instead of that one on greek indices a and b (from 0 to 3) in Eq. (24) :
Dgf = divg (gradg f) = (1/|g|) (¶/¶xi)( Ö|g| gij ¶f/¶xj)
. (25)
Due to this non-linearity, Eq.
(23) contains features of classical equations for intense wave propagation
(e.g. those of gas dynamics), in particular it contains the possibility of
shock waves (Sect. 8). There is another non-linearity in Eq. (23), since its
right-hand side already contains a non-linear dependence of pe on r; in a sense, this right-hand side implies that the
gravitation field, characterized by pe or re , is a source to itself. Moreover, the mass-energy
equivalence of SR has to be accounted for in the definition of the mass distribution
r. Thus r in Eq. (23) is defined to be the density
of mass-energy in the frame E. As imposed by the inclusion in r of the energy
of light-like particles (divided by c2), the mass of ordinary particles involved in r is not the
rest-mass but the velocity-dependent one, which is to say that the Newtonian
equality of active and passive gravitational mass is saved. It implies that the
mass equivalent of the ordinary, kinetic pressure p in macroscopic bodies is
included in r, in other words pressure does contribute to gravity in the ETG, as in
GR.
It appears that Eq. (23) has no covariance property, but
this is a priori tenable since all quantities are understood in the frame E, which
according to the theory is strongly privileged. The next thing to do is thus to
show that the Newtonian approximation, which for most of the reliable
observations is very accurate and which implies the Galilean invariance, is
recovered for weak and slowly varying fields in this modified ETG. In GR, such
fields are characterized by the property that one may choose the coordinate
system (xa) so that the
space-time metric g differs
from the Galilean one h (with hab = dab if a=0 and hab = -dab if a=1,2,3) only by evanescent terms : gab = hab + hab and moreover the derivatives ¶h/¶x0 , with x0=ct, are negligible as compared with the space
derivatives ¶h/¶xi.
Similarly, we admit that the field pe has the form
pe = pe¥(1-U/c2), U/c2 <<1 ,
(26)
and we will neglect the derivatives of the kind ¶pe/¶x0 with
respect to the corresponding space derivatives. Eq. (26) obviously means that
the gravitation field in the sense of the ETG (g in Eq. (5)) is weak; moreover, the deviations from the Euclidean
space metric g0 and the uniform time t are directly given by the
ratio pe/pe¥ (Eq. (16)). If we select a Cartesian coordinate
system (xi) on M, i.e. g0ij=dij , it follows thus from Eq. (26) that the Laplace
operator D according to g (Eq. (25)) will differ negligibly from that one
according to g0, D0 f=¶2f/¶xi¶xi, and that the derivatives with respect to the local time tx may be
replaced by ones with respect to the time t. If we account further for the
assumption of a slowly varying field, we rewrite Eq. (23) in the form
D0 pe = 4pG r re » 4pG r re¥. (27)
Now with pe = c2 re, the field g = - (grad pe)/re is, by Eq. (26), equivalent to -(grad pe)/re¥ , thus we recover the incompressible case with Euclidean metric, i.e.
the Newtonian equation for the gravitation field :
D0 U = - 4pG r . (28)
In other words U in Eq. (26) is equivalent to the Newtonian potential.
It may be worth to give a simple reason why the spatial derivatives should
dominate the x0-derivatives in
the Newtonian limit. The Newtonian potential is the convolution product : U=Gr*(1/r) with r
the spatial distance, so that:
grad U = G r * grad(1/r) ,
¶U/¶x0 = (1/c) ¶U/¶t = (1/c)Gr * ¶(1/r)/ ¶t = (1/c)Gr * [(¶r/¶t).grad(1/r)] , (29)
and -¶r/¶t in (29) is the velocity of the current point y in the set of massive bodies, with
respect to the point x where the
field is computed. Thus for low velocities one has |¶r/¶t| << c for any y and ¶U/¶x0 is
indeed negligible with respect to grad U.
The Newtonian field equation
(28) may be written in any reference frame (as far as the space metric is
considered Euclidean) and thus does not define the inertial frames. These are
obtained from the Galilean invariance of the non-relativistic Newton law; in
the ETG, the latter is derived in exactly the same way as in GR, from
Einstein's geodesic assumption for weak and slowly varying fields and small
velocities. In this derivation, the x0-derivatives of the metric are again neglected. Thus the approximate
inertial frames that appear for weak and slowly varying fields are such that
the corresponding expression of the metric is close to be static, as is
confirmed by the result (G). The basic assumption (A) (the gravitational space
contraction in the ratio b of Eq. (16)) relates the physical space metric in the
frame E to the abstract Euclidean metric which makes the
macro-ether a rigid body. Thus, in stating assumption (A) we force the ether to
remain the absolute space also in the modified version of the proposed theory;
moreover, the iterative approximation of the proposed ETG confirms that the
inertial frames of the first (Newtonian) approximation are in uniform motion
with respect to the macro-ether (this iterative scheme is not presented in this
paper).
Note that in the static
case (re time-independent), Eq. (23) implies
that r also does not depend on t in the frame E; since in that case the modified Newton law holds,
there can be only one body (any other body would fall, in contradiction with
the constancy of r) and this body must be in equilibrium and at rest in
the frame E. Thus in the static case there is no relative motion
of ether and matter at the macro-scale. There is another case where the
proposed ETG leads to this "total dragging" situation. We have
postulated a constitutive ether:
according to this, material (elementary) particles would be local flows in
ether [13]. If one accepts this, then the macroscopic motion of the ether
(defining the frame E) must include the motion of matter, since the former
motion is a weighting of the motions of the ether "constituting the
particles" and of the ether "outside the particles". As realized
above, the macro-ether remains the absolute space, hence the particles cannot
drag all the surrounding fluid. However, the mean motion of ether is directly
influenced by the motion of particles. Since the ether compressibility is
assumed to be extremely low (K=1/c2), the "amount" of ether inside the particles contained in a
volume W, mepart = òparticles in W re dV, is
nearly proportional to the volume they occupy, Vpart = òparticles in W dV. Hence, at ordinary densities where the particles occupy only a very
small volume fraction, the direct (kinematical) influence of the motion of
matter on the macroscopic motion of ether is likely to be very small. But
consider the case of a body in advanced gravitational
collapse, where the material density would be higher than the nuclear
density; in that case, it is natural to admit that the particles are
"contiguous to each other", i.e. that all ether is involved in
material particles : the macro-ether is then automatically comoving with matter
(see Sect. 8 for an application).
Go to the next section: “The modified Newton law
implies geodesic motion…”
Back to the beginning of the paper
REFERENCES for Sections 1 to 5
[1] A. Papapetrou,
Proc. Phys. Soc. A64, 57 (1951).
[2] V. Fock, The theory of space, time
and gravitation, Pergamon, Oxford 1964.
[3] T. Damour and N. Deruelle, Ann. Inst. Henri Poincaré
(Phys. Th.) 43 (1), 107 (1985).
[4] S. Weinberg, Gravitation and
cosmology, J. Wiley & Sons, New York 1972.
[5] A. A. Logunov, Yu. M. Loskutov and
M. A. Mestvirishvili, Sov. Phys. Usp. 31
(7), 581 (1988) (Transl. from Uspekhi Fiz. Nauk 155, 369 (1988)).
[6] D. W. Sciama, in "The
philosophy of vacuum" (S. Saunders & H.R. Brown, eds.), Clarendon
Press, Oxford 1991, p. 137.
[7] F.
Winterberg, Z. Naturforsch. 43a, 369
(1988).
[8] M. Arminjon, Rev. Roum. Sci. Techn.- Méc. Appl. 38, (a) 3 and (b) 107 (1993).
[9] L. Euler, Opera omnia, Ser. 3, i: Commentationes physicae, pp. 3-15
and pp.149-156 (1746).
[10] G. Builder, Austr. J. Phys. 11,
(a) 279 and (b) 457 (1958).
[11] S. J. Prokhovnik, The Logic of special Relativity, Cambridge
University Press, Cambridge 1967.
[12] A. Einstein, Sidelights on Relativity, Methuen, London 1922.
[13] L. Romani, Théorie générale de
l'univers physique (réduction à la cinématique), Blanchard, Paris 1975 (vol. 1)
and Paris 1976 (vol. 2).
[14] A.
Einstein, Ann. d. Phys. 38, 355 (1912).
[15] E. Soós, Rev. Roum. Sci. Techn.- Méc.
Appl. 37, (a) 127 and (b) 245
(1992).
[16] J. L. Synge, Relativity, the general theory, North-Holland,
Amsterdam 1964.