Energy
and equations of motion in a tentative theory of gravity with a privileged
reference frame
Archives of Mechanics (Warszawa) 48, No. 1, pp. 25-52 (1996)
M. ARMINJON (GRENOBLE)
Abstract- Based on a tentative interpretation of gravity as a
pressure force, a scalar theory of gravity was previously investigated. It
assumes gravitational contraction (dilation) of space (time) standards. In the
static case, the same Newton law as in special relativity was expressed in
terms of these distorted local standards, and was found to imply geodesic
motion. Here, the formulation of motion is reexamined in the most general
situation. A consistent Newton law can still be defined, which accounts for the
time variation of the space metric, but it is not compatible with geodesic
motion for a time-dependent field. The energy of a test particle is defined: it
is constant in the static case. Starting from ‘dust’, a balance equation is
then derived for the energy of matter. If the Newton law is assumed, the field
equation of the theory allows to rewrite this as a true conservation equation,
including the gravitational energy. The latter contains a Newtonian term, plus
the square of the relative rate of the local velocity of gravitation waves (or
that of light), the velocity being expressed in terms of absolute standards.
1. Introduction
AN ATTEMPT to deduce a consistent theory of gravity
from the idea of a physically privileged reference frame or ‘ether’ was
previously proposed [1-3]. This work is a further development which is likely
to close the theory. It is well-known that the concept of ether has been
abandoned at the beginning of this century. It is less widely known that, in
the mean time, the objective situation in physics has made it reasonable and
interesting to reexamine this concept. In such a matter, it is necessary for
the writer to appeal to authorities. Thus:
(i) Due to the work of BUILDER [6-7],
JANOSSY [11], PROKHOVNIK
[21,23], it has now been proved in detail that special relativity (SR) is,
after all, fully compatible with the
assumption of the ether as envisaged by Lorentz and Poincaré, i.e. with the
ether being an inertial frame in which Maxwell’s equations can be written and
relative to which all material objects undergo a ‘true’ Lorentz contraction. This
has been emphasized by physicists as important as BELL [4],
the author of theorems on ‘hidden variables’ in quantum mechanics. In a recent
review on the latter subject, MERMIN [17]
writes: « What Bell’s Theorem did suggest to Bell was the need to reexamine our understanding of Lorentz invariance »
(italics ours). It is worth to recall that several basic results of SR,
including the Lorentz transformation and the Lorentz invariance of Maxwell’s
equations, were found by Lorentz and Poincaré, prior to Einstein, within a theory based on ether. As stated by BELL [4],
the main differences between the approaches by Lorentz (and Poincaré) and by
Einstein are that: (a) « Since it is experimentally impossible to say
which of two uniformly moving systems is really
at rest, Einstein declares the notions ‘really resting’ and ‘really moving’ as
meaningless. » (b) « instead of inferring the experience of moving
observers from known and conjectured laws of physics, Einstein starts from the hypothesis that the laws will look the
same to all observers in uniform motion. » (italics are Bell’s). It is now
accepted that the Lorentz-Poincaré opposite philosophy leads to the same
physical theory, namely SR.
(ii) It has become evident that quantum mechanics leads to attribute
definite physical properties to the so-called ‘vacuum’, and that these
properties do affect our measuring instruments as predicted by quantum
mechanics. As SCIAMA [25] states:
« For example, the electric and magnetic fields in the electromagnetic
vacuum are fluctuating quantities. This leads to a kind of reintroduction of
the ether, since some physical systems interacting with the vacuum can detect
the existence of its fluctuations. However, this ether is Lorentz-invariant, so
there is no contradiction with special relativity. »
(iii) Finally, relative velocities of astronomical objects are being
measured with increasing accuracy. We can associate a privileged reference
frame with the ‘cosmic fluid’, the velocity of which is the average velocity of
matter. This reference frame appears clearly in the cosmological models
because, in these simplified models, our universe is assumed homogeneous so
that the average is already done. For example, the Robertson-Walker space-time
metric of an expanding universe distinguishes a particular class of ‘comoving
observers’- that is, comoving with the expansion commonly assumed to explain,
as a Doppler effect, the observed red-shift of the spectra emitted by distant
galaxies. Their set makes a privileged reference frame, as emphasized by PROKHOVNIK [21-22].
Thus,
we have a privileged reference frame in which also the ‘empty’ parts have
physical properties. This may be called an ‘ether’ for short, even though
‘physical vacuum’ would be more appropriate. The use of the old name does not
imply to forget modern physics: but that precisely today's physics allows to
reconsider the assumption of an ‘ether’, provides some justification for
reconsidering also the possibility
that, after all, the allegable existence of this ‘ether’ might manifest itself in certain laws of physics. Since the
privileged reference frame is kinematically defined from the average motion of
matter at a very large scale, gravitation could be the range of such speculated
manifestations. In other words, it seems allowable to investigate a theory of
gravity with a privileged frame, one which would not necessarily be neutral in
the theory: a non-covariant theory. Some important astronomical facts at the
scale of galaxies, such as the famous rotation curves in the disc galaxies,
have not yet received any undebatable interpretation [19,30]. Hence an
explanation deriving from the effect of motion through an ‘ether’ might be
considered.
However,
Newtonian gravity (NG) gives an excellent description of astronomical motions
at smaller scales, which is even refined by the corrections of general
relativity (GR). Since neither NG nor GR does admit a preferred reference
frame, it is undoubtedly a risky affair to attempt the construction of a theory
of gravity with such a frame. A such attempt has yet been proposed [1-3]. The
aim was to investigate whether the ‘logic of absolute motion’, which furthers
our understanding of special
relativity (SR) as compared with the usual ‘space-time logic’ [4,21], can be
extended so as to build a sensible theory of gravity. The investigated theory is non-linear, like GR, and
coincides with NG at the lowest approximation, also like GR. As an argument in
favour of giving some attention to this theory, we mention the analytical study
of the gravitational collapse in ‘free fall’ with spherical symmetry, i.e. the
situation analytically studied within GR by OPPENHEIMER &
SNYDER [18]. Since then, it has been shown, notably by PENROSE [20], that this situation contains all essential
features of gravitational collapse for very massive objects in GR. According to
the investigated theory, no singularity occurs during this collapse, neither
for the metric nor even for the energy density, because the implosion would
stop within finite time (for freely falling clocks and for remote clocks as
well) and would be followed by an explosion [3]. On the other hand, this theory
gives exactly the same predictions as GR for the motion of a test particle in
the assumed static gravitation field of a spherical body, for in that case the
Schwarzschild space-time metric of GR is obtained and the Newton law of the
theory implies geodesic motion for any static field. The last result applies to
mass particles [2] and to light-like particles as well [3], and provides a link
between dynamics in NG and in GR, in the sense of MAZILU [16].
In this non-covariant theory, however, a gravitation field is static only if
its source, the mass-energy density in the frame bound to ‘ether’, is
time-independent. Whereas in NG and GR a uniform motion of the massive body can
be eliminated by changing the reference frame, this is not the case here. Thus,
in order to analyse either planetary motion in the solar system or stellar
motion in a galaxy, one might have to reckon with velocities in the range 100-1000
km/s.
In
the previous work, a Newton law has been defined only in the static case. Since
it then implies geodesic motion, geodesic motion has been assumed in the
general case. The purpose of this paper is to study in greater depth the
formulation of motion in the theory, in connection with the problem of energy.
We first recall (Sect. 2) the basic principles and equations of this theory,
obtaining an alternative (equivalent) form of the field equations. For the
equations of motion (Sect. 3), it is shown that in the general, non-static
case, a consistent Newton law can still be defined, but is incompatible with
the geodesic formulation of motion. Then the energy problem in the theory is
analysed (Sect. 4). As is known, an exact energy can hardly be defined within
GR, since the obtainment of a conservation equation for energy-momentum asks
for a privileged class of reference frames (see e.g. STEPHANI
[28]). After having recalled some aspects of the question of gravitational and
total energy in NG and in GR, it is shown that a local energy balance equation,
including the gravitational energy, is obtained with the studied theory if one
assumes the (extended) Newton law of motion, but not under the geodesic
formulation of motion.
2. Basic assumptions and equations
2.1 Absolute space and physical vacuum
Since astronomical observations and
the success of Newtonian theory suggest that Galilean space-time is a very
accurate description of our real world-theater, the notion of a physical vacuum
has first to be conciled with classical
mechanics. This, however, was not accomplished by ether theorists. For the
ether must be the absolute space, hence rigid- otherwise, one would have two independent absolute spaces. But it
also must offer no resistance against motion, and this in Newtonian mechanics
can be true only of a perfect fluid. The proposed answer is that it is the average motion of the hypothetical
perfect fluid that defines the privileged inertial frame [1-2],
corresponding to the absolute space of Newtonian theory. Since any motion must
be referred to some space (and time), it may seem that we are lead to a vicious
circle. Thus we first postulate the absolute space or 3-D manifold M, which as a working assumption we may
take to have Euclidean structure[1]. And
we postulate the absolute time t,
i.e. the world of events M 4
(time and position) is assumed to be the product RxM [2]. In
Newtonian theory, the natural space metric g0 on M and the absolute time are assumed to
be experimentally accessible, independently of motion and gravitation. In the
studied non-linear theory, the coincidence between ‘absolute’ space (or time)
metric and physical space (or time) measurements is found only in the first
approximation. Then we may define the motion of a continuous medium, relative
to M, by its velocity vector field v0 = dx/dt. The particular
metric structure we assume for M
ensures that the integral of a vector field makes sense and is a vector (note
that it is not the case for a general
Riemannian space and thus for GR). Hence, the volume average of the velocity in
any finite domain W occupied
by the continuous medium is well defined, say 
. Now we may precise the assumption according to which
the ‘microscopic ether’, that one which would be a perfect fluid, has in the
average no motion relative to the absolute space M : we suppose that the velocity field of the micro-ether, v0e, is everywhere defined (it fills the space) and is such
that 
® 0 as
the size of the regular domain W (let us say it is a ball)
infinitely increases, and this independently of the spatial position of W. We
may call M the macro-ether.
Since
the micro-ether must fill the space, any kind of matter, made of material
particles, should be actually made of this universal fluid. Thus, material
particles should be local, organized flows in ether, such as vortices which in
a perfect fluid can be everlasting. We note that this concept is compatible
with the lack of complete separability between particles, which is predicted by
quantum mechanics and has received experimental confirmation. It would be an
ambitious program, however, to attempt recovering micro-physics from this
assumption of a ‘constitutive ether’
(but not a hopeless program: cf. the hydrodynamic interpretation of
Schrödinger’s wave equation by MADELUNG [15];
more recently, ROMANI [24], WINTERBERG [31-32] and DMITRYIEV [9]
obtained results in the same direction). Anyway, the gravitation theory needs
almost only the macro-ether, which will be physically defined from the average
motion of matter, i.e. the average
motions of ether and matter are assumed identical. Recall that the notion of
average used in this definition, is the asymptotic volume average. This means
that no a priori bound needs to limit the size of local inhomogeneities, i.e.
the size of astronomical structures.
2.2 Scalar field equation and space-time metric
A perfect fluid can exert only
pressure forces. The gravitation force is tentatively interpreted as the
pressure force or Archimedes' thrust, resulting from the gradient of the
macroscopic pressure pe in
the ether. This gives the following expression for the gravity acceleration g [1] :
(2.1) 
where re is the macroscopic density of the hypothetical fluid,
assumed barotropic; the latter means that re depends only on pe,
it is imposed to a true ‘perfect’ fluid which should be continuous at any
scale, so that no temperature and no entropy can be defined [24]. The
interpretation leading to Eq. (2.1) must be qualified as tentative in so far as
it is based on the assumption that a micro-ether (or physical vacuum, or
subquantum medium) does exist as a perfect fluid, whereas a consistent theory
of microphysics following this line, still remains to build. In this
interpretation, the gravitation force can be seen as a correction, i.e. it is
what would remain when the microscopic fluctuations of ether pressure, which
should be responsible for the other three forces, would have been accounted
for. Although it is derived from this tentative interpretation, we take Eq.
(2.1) firmly, but as a phenomenological
equation in which pe plays
the role devoted to the Newtonian potential U
in NG; it is thus substituted for
g = grad U.
Just like for the latter, the macroscopic nature of Eq. (2.1) (the fact that
the involved fields vary significantly over macroscopic distances only) does
not prevent g from being felt at the
scale of material particles.
The
field equation for pe,
playing the role of Poisson's equation for U,
is written as:
(2.2) 
with D the Laplace
operator, r the density of matter (the density of the conserved
mass in the first, Newtonian approximation; in the non-linear theory, r is the mass-energy density in the frame E in which the points of M have no motion[3]), tx
a local time to be precised
hereafter, and G Newton's gravitation
constant. It is obtained basically from four requirements:
(i) Since NG propagates with
infinite speed, it must correspond to the case where the fluid is
incompressible, re =
Const., and the field equation must become equivalent to Poisson's equation as
the compressibility evanesces.
(ii) In the compressible case,
pressure waves must appear (except for static situations where pe does not depend on time),
the velocity ce of which
will be determined by the local ether compressibility,
K = 1/ce2
= dre/dpe.
(iii) Accounting for SR in the
Lorentz-Poincaré interpretation thoroughly developed by PROKHOVNIK [21,23], the velocity of light, c, becomes a limiting speed: so should be also the velocity of the
pressure waves (the ‘sound’ velocity) in the assumed constitutive ether, hence
one must have ce = c everywhere (this implies that the
barotropic relationship between pe
and re is linear,
pe = c2
re).
(iv) In the theory, the equivalence
principle arises naturally, as a correspondence between the absolute metric
effects of motion and gravitation. As a consequence, the space (time) standards are assumed to be contracted (dilated) in
the gravitation field, in the ratio b = pe/pe
, where pe
is the value of pe
in regions which are remote from any matter and hence free from gravitation
(see footnote 4, however); the space contraction occurs only in the direction
of the gravity acceleration g. Hence,
the ‘physical’ space metric g in the frame E
becomes distorted, as compared with the metric natural g0, and the grad operator in Eq. (2.1), as well as the Laplace operator in Eq. (2.2), are in terms of the curved physical
metric g:
(2.3) (grad f)i = (gradg f)i
= gij 
, (gij) º g-1
(2.4) D f = Dg f = divg gradg f = 
, g = det (gij).
Moreover, a local time tx
appears at any fixed point x in M; thus if the point x0, also bound to M, is far enough from any matter so that
no gravitation field is felt at x0:
(2.5) dtx/dt = dtx
/dtx0 = b = pe(t,x)/pe(t,x0) , b = pe/pe
<1 ,
whence the definition of the
derivation with respect to local time, appearing in Eq. (2.2):
(2.6) 
,
with tx0
= t if is x0 is ‘far enough’, i.e. if pe(t,x0)
pe
. Note, however, that Eq. (2.6) assigns a unique value
to any derivative with respect to local time, 
, even if one changes the reference point x0 in M, and this whether x0
is ‘far enough’ or not.
The
assumed contraction of the physical space standards (and thus the dilation of
measured distances), with respect to the natural metric on M, occurs in the direction of the gravity acceleration g. Hence the expression of g, the
physical space metric in the frame E, is the simplest
in an ‘isopotential’ coordinate system. This is a space-time coordinate system
(ya) such
that, at any given time t, y1=Const.
(in space) is equivalent to pe=Const,
and such that the natural metric g0 is diagonal: (g0ij) = diag (a01, a02, a03). In such a
system, the gravitational space contraction implies that g also
is diagonal, and writes:
(2.7) (gij) =
diag (
a01, a02, a03) 
diag (ai)1 £ i £ 3 (isopotential system), b = pe/pe
.
(Greek indices will vary from 0 to 3
and Latine ones from 1 to 3). Note that, in the general case where pe depends on the time t, a such system will usually not be
bound to the frame E, i.e. a point x
in M will in general have
time-dependent coordinates yi(t,x). An important exception is the case
where one has spherical symmetry around a fixed point x0 in M (this
either implies that (M,g0) is
Euclidean, or must be understood locally). Then, the time t makes with the spherical coordinates r, q, f an isopotential
coordinate system bound to E.
The
line element of the space-time metric g, measuring the
proper time dt along
an element of trajectory, follows straightforwardly from the combination of the
slowing down of the mobile clock due to its absolute motion and to the
gravitation field [2]. If dl is the
line element of the space metric g, i.e. if dl
is the elementary distance covered by the mobile, as measured with rods of the
momentarily coincident observer bound to E, one
has:
(2.8) ds 2 = glm dxl dxm = c2 dt 2 = b 2 (dx0)2 - dl 2, x0
= ct , dl 2 = gij dxi dx j.
The validity of Eq. (2.8)3
assumes that the coordinates (xa) are
bound to the frame E. By Eq. (2.7), a diagonal expression is hence
obtained also for g in the particular case where an
isopotential coordinate system bound to the frame E can be found. In that case:
(2.9) (glm) =
diag (b 2 , -
a01 , - a02 , - a03) 
diag (bl)0
£ l £ 3 .
If general coordinates (za) are
used, one writes instead of Eq. (2.8)3:
(2.10)
dl 2 = dtx2
gij v i v j = dtx2
v2 ,
with vi the components of v = dx/dtx
= (1/b) dx/dt (v
is the velocity vector with respect to E and
using the local time of the momentarily coincident clock of E) in
the coordinates (zi)
(these being considered, at given time t,
as a space coordinate system, thus
if the (xa) are
bound to E). Of course, g is a space-time
tensor and may be written in any space-time coordinates (za). Also, a space metric h can
be defined in the frame F bound to such coordinates, from the metric g: the
components of the inverse matrix h-1 are
hij = - g ij, with (glm) the
inverse matrix of (glm). As shown by LANDAU & LIFCHITZ [12],
the metric h is that one which gives the distances between
neighbouring points bound to F (i.e. having constant space coordinates zi ), as evaluated from the
interval of their local time, dt, for
a to-and-fro light path:
dl ’ = (hij dzi dzj )1/2 = c dt/2. Since
SR still holds locally in the presence of gravitation, the result of PROKHOVNIK [21] is valid, according to which dl ’ is indeed the physical distance
which may be measured with rods of the frame F .
2.3 Expression of the field equation in terms of natural metric and
absolute time
The expressions of the ‘main’ field
equation (2.2) and the ‘auxiliary’ one (2.1) are in terms of the physical space
metric and local (physical) time, in the frame bound to the absolute space or
macro-ether M (it is recalled that
Eq. (2.2) is only valid in this frame E). However, this
physical space-time metric depends on the unknown, i.e. on the field pe. In some cases, it is
easier to handle Eq. (2.2) when it is expressed in terms of the natural metric g0 and
absolute time t, as this turns out to
be possible. Starting from Eq. (2.1) with
pe = c2re, we use isopotential coordinates (ya) and
Eqs. (2.7) and (2.3), and obtain, since pe
or b
depends only on y1:
(2.11) 
where (ei) 1 £ i £ 3 is
the natural basis associated with the coordinates (yi). Thus:
(2.12) 
=(g00)E
(that (g00)E =b 2 if
one uses the absolute time coordinate t,
is due to Eq. (2.8)1). Turning to Eq. (2.2), we have g º det (gij) = g0/b 2 from (2.7), thus
we first obtain in the same way:
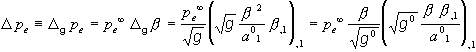
(cf. Eq. (2.4)), which may be
rewritten as:
(2.13) 
.
Now, let us assume that our (model
of) universe, in which the studied gravitation field and matter are embedded,
is ‘static at infinity’, which is likely to be an extremely good approximation-
except for cosmological problems. That is, assume that 
is independent
of the time t [4]. In
that case, the term with time derivatives in Eq. (2.2) becomes:
(2.14)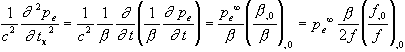 
.
Combining Eqs. (2.13) and (2.14) and
multiplying by 2/(b
), we rewrite Eq. (2.2) as:
(2.15)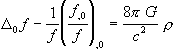 
.
Thus,
the field equation reduces in the static case to the ordinary Poisson equation,
which is linear, and indeed Eqs.
(2.12) and (2.15) are equivalent, for time-independent f (and r), to the Newtonian equations:
exactly the Newtonian gravity acceleration
g will be associated with any given density of mass-energy, r(x), by Eqs. (2.12) and (2.15). However,
in NG, only the ‘invariable’ (rest) mass is counted in r ;
moreover, it remains to precise the definition of r, and it turns
out that r must depend on the gravitation field, i.e. on f itself [Sect. (4.2), point (iv)].
Anyhow, not the same motion will be predicted for test particles if g is known, since in the studied theory
Newton's second law is expressed in terms of space and time measurements with
clocks and rods of the local observer in E,
which are affected by the gravitation field. In the static case with spherical
symmetry, for example, Eq (2.15) (plus the requirement that g remains bounded as r ®0, or the boundary condition f=1 at infinity), gives f = 1- 2 Gm/(c2r) outside the body (r being the radial Euclidean distance,
and with
(2.16) m = òM r dV 0.
where dV 0 is the volume element of the Euclidean metric).
Then Eq. (2.9), with a01
=1, a02 =r2 and a03 = r2
sin2q in spherical coordinates r,q,f,
leads to Schwarzschild's exterior space-time metric. It is striking that, after
natural account of SR and the equivalence principle, this theory (to which we
have imposed to reduce to NG asymptotically as the ‘ether compressibility’
evanesces), gives exactly and simultaneously the Newtonian attraction field g and the Schwarzschild metric in the
spherical static case [2]. The new result is that the Newtonian g-field is predicted for any static
situation, whether ‘spherical’ or not. The form (2.15) of the field equation
has important applications also in the non-static case, see Sect. 4.2 (energy
balance).
3. The motion of a test particle: Newton law vs. space-time geodesics
To state Newton's second law demands
to define the acceleration or rather (since SR must be taken into account) the
time derivative of the momentum. Also because SR must hold at the local scale
(and for sure with physical space-time metric), one has to use the physical,
distorted space and time standards, i.e. the Riemannian space metric g and
the local time tx.
3.1 The case of a time-independent spatial metric g (static gravitation field)
If on a manifold M a Riemannian metric is given (thus a fixed metric g), one has a natural definition of the ‘time’
derivative of a vector u(t) attached to a ‘trajectory’ i.e. a
differentiable mapping t a X(t)
from an open interval in R into M. The
components hi of
the derivative Du/Dt in a local
coordinate system (xi) on M are given by:
(3.1) hi = 
,
with 
the second-kind Christoffel symbols associated with
metric g in coordinates (xi)
and v0k = dxk/dt
= (dx/dt)k the
components of the ‘velocity vector’ (with respect to the ‘time’ t which in (3.1) may be an arbitrary
parameter, although in the rest of the paper t denotes the absolute time). The definition (3.1) may be found in
the literature, e.g. in BRILLOUIN [5]
and in LICHNEROWICZ [13] where it is induced from that
of a covariant derivative. However, a covariant derivative demands, strictly
speaking, that u be a vector field
(defined in an open domain around the considered point X), whereas here u is
only defined along the trajectory, as a function of the parameter t (and this, of course, is what is
needed to use Eq. (3.1)). On requiring that the derivative Du/Dt cancel for any parallel vector and be a true derivative, i.e.
obey the Leibniz rule, one is lead uniquely to characterize Du/Dt by the following intrinsic property:
(3.2) for
any vector w in the tangent space TMX at point XÎM, 
,
where point means scalar product g and w’ is the parallel transport (using g) of
vector w on the trajectory [2];
moreover, the components of the vector
Du/Dt defined in this way, are indeed
given by Eq. (3.1). Note that here M
is also equipped with the Euclidean
metric g0 which
would allow to speak of ‘a vector v
in M ‘ (i.e. not specifically
attached to a point XÎM), and in fact to identify points in M and vectors (once an arbitrary origin
point OÎM has been selected) [5],
whence our notation xÎM in previous sections. Thus the Newton law of SR has
been extended to this theory of gravity, in the form:
(3.3)
F º F0 + m(v) g = 
,
(3.4)
where F0 is the non-gravitational (e.g. electromagnetic)
force, 
is the
velocity of the test particle with respect to M,
v = g(v,v)1/2º(gij vi vj)1/2
its modulus and
m(v)=m(0)/(1-v2/c2)1/2 is the inertial mass, which is thus
identical to the passive gravitational mass, as is also true in NG. Although
the latter identity is often referred to in GR (under the name of ‘weak
equivalence principle’), it does not make an exact sense in GR, because there
is no Newton law there [27]. The Newton law (3.3) is also defined for light-like particles (photons,
neutrinos?), in substituting the energy e=hn (or
rather e/c2) for the
inertial mass.
3.2 Extension to the time-dependent situation
In the general case, the metric g will
yet depend on the time t (i.e. its
components gij in
coordinates bound to E will depend on t),
hence it seems at first that Eq. (3.2), which is at the root of the definition
of the time derivative of the momentum, used in Eq. (3.3), does not make sense
any more: how can one define a parallel transport with respect to a metric that
varies, i.e. with respect to a one-parameter family of metrics? Thus it seems
at first that the Newton law (3.3) makes sense only for static gravitation fields, and so was it defined and used in the
previous work [2-3]. However, it turns out that Eqs. (3.2)-(3.3) do still make
sense, provided one ‘freezes’ the space metric 
of the time t0 where the derivative is to be calculated.
In order to calculate the derivative DP/Dtx of the momentum P=m(v) v,
one thus might use Eq. (3.1) (with P
in the place of u and the local time
tx
in the place of t) where the G symbols refer to the metric 
. A natural definition of the parallel transport w’ in Eq. (3.2) can indeed be given
only if one considers the fixed metric 
. But this observation does not completely solve the
question on the extension of Eq. (3.2) to the case with time-dependent metric gt: it remains to
investigate whether the scalar product on the right of Eq. (3.2) should also
refer to the fixed metric 
, or instead to the time-dependent metric gt. If we take 
, we define from (3.2) a derivative D0u/Dt for which the
Leibniz rule and Eq. (3.1) hold true, but clearly we are missing something,
namely the time variation of the physical metric gt. If we take gt and
reexamine the derivation of Eq. (3.1) from Eq. (3.2) (Appendix 1 in [2]) we
easily obtain, instead of (3.1):
(3.4)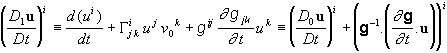 
,
where, for a twice covariant
second-order tensor h (here
) and a vector u,
h.u is
the covector with components hij
u j. And, for a twice contravariant second-order tensor k (here
g-1) and a covector u*, k.u* is
the vector with components kij
u*j.
Thus, Eq. (3.4) also defines a vector
D1 u /Dt. Yet
this time derivative, which accounts for the time variation of the metric, does
not cancel for a vector u that is
transported parallel to itself (necessarily with respect to the fixed metric 
) along the trajectory. The use of Eq. (3.2) for the
definition is hence questionable, since Eq. (3.2) was obtained (in the case of
a fixed metric) under the former requirement, plus the condition that the
Leibniz rule has to be verified. If we provisionally forget the Leibniz rule,
we can therefore define a one-parameter family of vector time-derivatives as
well:
(3.5)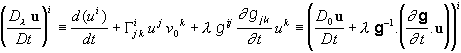 
(that D0 u /Dt enters the definition (3.5) with
the coefficient 1 is enforced, since we want to recover Eqs. (3.1) and (3.3)
for a time-independent metric). Now let us come to Leibniz' rule. We obtain
from Eq. (3.5) and the fact that, by construction, D0u/Dt obeys the Leibniz rule with the
fixed metric 
:
(3.6) =
+ 2 l 
.
But, by direct calculation, we also
have:
,
(3.7) 
= 
+ 
.
By comparing (3.6) and (3.7), we
find that Leibniz' rule holds (with the
variable metric gt) if and only if l=1/2 in Eq.
(3.5). Nevertheless, with any value of l, we may
associate a particular Newton law, in the following way:
(3.8) F º F0 + m(v) g = 
, 
.
Now
is l=1/2
really the correct value for the parameter l? Another
possible criterion for the choice could be the compatibility of Eq. (3.8) with
the formulation of motion in GR. It has been proved that, in the static case, the Newton law (3.3) implies that any free test particle follow a geodesic line of the
metric g, and this for a mass particle [2] as well as for a
light-like one [3]. It is not difficult (though a bit tedious) to follow the
proof for a mass particle in the static case, the calculation method also
applying to the case where one still has isopotential coordinates bound to E. One
then finds that, already in that particular case, any time dependence of the
field pe makes new terms
appear in the geodesic equation for the values 0 and 1 of index a,
corresponding to new non-zero Christoffel symbols of metric g in
isopotential coordinates; and these new terms imply that, for a=0 and
a=1,
this equation Ga = 0
is verified if and only if l=1. The a=0 term will be
examined indirectly in Sect. 4.2 (in connection with the energy balance). In
summary, we presently cannot state for sure that the Newton law (3.8) with l=1
implies geodesic motion in the most general case, but we already know that the law (3.8) with any l¹1, in particular with l=1/2 (as is
needed to have Leibniz’ rule) is
incompatible with geodesic motion. Here is thus a crucial bifurcation in
the studied ether theory: one has to
decide between Newton law (with Leibniz rule, thus l=1/2) and space-time geodesics. In our
previous work, the second choice had been made. This choice is consistent with
the commonly accepted ‘logic of the space-time’, but this was not the main
reason for the choice: simply, no other possibility had been seen! From a
rather philosophical point of view, the first choice would be in fact more consistent
with the ‘logic of absolute motion’ which is studied here (cf. PROKHOVNIK [21] for a detailed discussion of the two different
‘logics’ in the frame of SR). The agreement with observation might be the true
judge between the two possibilities, both of which are indeed compatible with
the kernel of the studied theory (summarized in Sects. 2.1 and 2.2) from a
purely physical viewpoint. A strong physical argument for the choice ‘Newton
law’ (with l=1/2) and against ‘Einstein geodesics’ within the
studied theory will, however, appear in Sect. 4.2.
4. The energy problem in the studied theory of gravitation
4.1 Some remarks on energy and conservation laws in Newtonian theory and
in general relativity
(i) Is the concept of energy a relative one?
The concept of energy is among the
most important one in today's physics, especially in classical physics
(classical mechanics of mass points and continuous media, thermodynamics,
classical electromagnetism) and in microphysics as well, but the notable
exception is the gravitation theory (GR): there, this concept can have only an
approximate status since it is not a covariant concept. Already in NG, the
(kinetic plus potential) energy of a mass point, e = (v2/2 - U)m,
is not even a Galilean invariant. Indeed, v
is obviously not invariant,
whereas the potential is a Galilean invariant, since both
Poisson's equation and the merely spatial boundary conditions, e.g. rU and r2.grad U
bounded at infinity, are so (it is recalled that strict NG imposes a spatially
bounded distribution of mass). That e
is changed by a constant when changing the inertial frame makes, of course, no
problem in NG since only the variations of e
are relevant there. But since NG demands a bounded mass distribution, the
energy in the frame of the mass-center could
be preferred on theoretical grounds, and is indeed preferred in actual
analyses: in classical mechanics, be it celestial or terrestrial, one considers
an assumed isolated system and one refers the velocity, and hence the kinetic
energy, to the mass center. Strictly speaking, one should consider an
(approximately) isolated subsystem of the assumed bounded universe and, for
elements of the subsystem, evaluate their velocity in the global mass-center
frame. But this would differ by a definite
constant (the velocity of the mass center of the subsystem) from the velocity
in the frame bound to the mass center of the subsystem. Thus in NG (and in the
same way in a good part of classical physics), an absolute concept of energy is
allowable, probably favourable indeed (cf. the definition of temperature in
statistical thermodynamics, as a mean kinetic energy). Apart from this, it
seems that, in non-relativistic quantum mechanics, one would prefer to avoid
discussing the effect, on the energy levels, of changing the reference frame.
It may be that in quantum mechanics also, an absolute concept of energy would
be favourable.
(ii) Energy and conservation laws in Newtonian gravity
In addition to this (debatable)
absolute character, a still more important (and undebatable) aspect of the
energy concept is that, in classical physics, it gives rise to local balance equations for continuous media,
which lead to global conservation laws.
We take the example of NG, which is relevant here, and we assume elastic
behaviour for simplicity (this includes the case of a perfect barotropic
fluid). Thus one has, in NG, the following definition and conservation equation
for the volume density w of the total
energy, i.e. the energy of matter (including its potential energy in the
gravitation field), wm
, plus the energy of the gravitation field itself, wg :
(4.1) w = wm + wg , wm = r (v2/2
+ P - U),
wg = 
,
(4.2) 
= 0 ,
with s the stress tensor and P the
mass density of elastic energy; this is derived from the more usual energy
balance (in which the energy wg
does not appear and a source term r
U/
t
remains), by using Poisson's equation. Upon integrating Eq. (4.2) in the whole
space and since the matter distribution is spatially bounded, one obtains the
energy integral in two successive forms, by using the fact that the field g is O(1/r2) at
large r and 
U/
t tends
towards 0 at large r:
(4.3) Em + Eg
º 
(4.4) Em + Eg
= 
.
These equations allow a clear
analysis of the energy transfer from matter to gravitation field and, inside
the contribution of matter, from potential to kinetic and internal energy.
Thus, starting from an ‘unbound’ state in which both the (positive) gravitational energy and the (negative) potential energy Ep = ò-rU dV are closer to zero than in the
final state, a gravitational concentration of matter will increase the
gravitational energy Eg
and thus decrease the total energy of matter, Em, Eq. (4.3). But since wm includes the potential energy, the decrease in Em is only due to the
decrease in Ep, dEp, and the ‘pure’
(internal plus kinetic) energy of matter is in fact increased by the amount - dEp /2, Eq. (4.4).
There is also a conserva-tion equation for momentum in NG, namely:
(4.5) 
,
[here uÄv is the tensor product, thus
(uÄv)ij
= ui v j ;
the vector operator div means the Euclidean divergence of a
second-order space tensor t, with
(div t)i = tij, j
in any coordinates deduced from
Cartesian ones by a linear transformation; and I or d is the identity tensor, Iij = d ij]. This is the
mere rewriting, using the Poisson and continuity equations, of Newton's second
law for the continuous medium: Poisson's equation implies that the last term in
Eq. (4.5) is simply -rg. But,
contrary to Eqs. (4.3)-(44) in which the energy of the gravitation field does
influence the global balance, the integration of Eq. (4.5) in the whole space
gives nothing else than the standard conservation of the total momentum of
matter. In other words: in NG, the
gravitation field has energy and this is positive, but it has zero total
momentum. Equations (4.4) and (4.5) are given in CHANDRASEKHAR
[8] though Eq. (4.5) is there in a form which is similar to the
‘conservation equation’ for the mass space-time tensor T of GR,
(4.6) [divg T] a ºTab;b = 0.
(iii) General relativity
With Eq. (4.6) appears the problem
of energy and conservation laws in GR. As explained by LANDAU & LIFCHITZ [12],
it « does not in general express the conservation law of anything »
(§101), i.e. it cannot be considered as a true conservation equation. The
reason is that no Gauss theorem applies to the divergence of a second-order
tensor in a curved Riemannian space (see also STEPHANI
[28]). In several relevant situations, including that of an asymptoti-cally
flat metric g (i.e. a space-time that is Galilean
at infinity), Eq. (4.6) nevertheless implies integral conservation laws. In
order to obtain such laws, one rewrites Eq. (4.6) in the form of a divergence
with respect to a flat space-time metric g0, by
adding to T a so-called
‘energy-momentum pseudo-tensor of the gravitation field’, t (the expression of which is not unique), thus :
(divg0 q)a º q ab, b = 0, q º (-g) (T +
t) (4.7)
(the factor -g is
there for reasons which are bound to the form of the field equations in GR).
That the space-time may be equipped with a global flat metric is, of course, a
strong topological assumption; in general, the discussion here is valid in the
domain W where the coordinate system (xa) in Eq. (4.7)1 is
regular, and the metric g0 can be defined by: g0ab= hab (=el dal
db l with e 0 = 1, e i = -1
for i=1,2,3) in these coordinates.
Anyway, in GR, the choice of the ‘background’ metric g0
(local or global) cannot be imposed. The first equation remains valid in any
coordinates deduced by a linear transformation from Galilean coordinates of the
flat metric g0, and the
definition of (any) t in GR makes t a tensor only under linear coordinate
transformations. Due to the factor -g, the definition of q and
the whole set (4.7) are hence covariant only for those transformations from
Galilean coordinates of the metric g0 that are both
linear and ‘unimodular’, thus essentially for Lorentz transformations of the
space-time (or the domain W) equipped with the flat metric g0. In
particular, the expression of (any) t
gives zero in locally geodesic cordinates for the curved metric g.
These peculiarities allow to state that « it is doubtful that [one of such
pseudotensors t, namely that
proposed by Einstein] can in general describe something which could be called
energy » (TRAUTMAN [29]). If the q ab ‘s decrease sufficiently fast at infinity[6] (this
implies in particular that the metric g asymptotically
coincides with the flat one g0, thereby
ensuring an ‘asymptotic uniqueness’ to g0, in
so far as the metric g of GR may be considered unique),
the integration of Eq. (4.7) over the whole ‘space’ (spatial section x0 = Const. of the
space-time) is possible and gives, owing to the Gauss theorem:
Pa º 
q a0 dx1 dx2 dx3 = Const. (4.8)
This is sometimes interpreted in GR
as the conservation law for energy (a=0) and momentum (a=1,2,3;
see e.g. LANDAU & LIFCHITZ
[12]). In contrast to Eqs. (4.3)-(4.4), however, the complex expression of
pseudo-tensor t in terms of
derivatives of the metric makes it difficult to draw definite conclusions from
Eq. (4.8), regarding the energy transfer. Moreover, it does not seem completely
clear what should be the physically motivated conditions ensuring the
sufficient decrease at infinity for q. Thus if one assumes a
‘time-independent far field’, one finds that Pi=0 and that P
0 is the active mass entering the expression of the metric at large
distance (cf. STEPHANI [28]). But,
strictly speaking, only a constant gravitation field, thus without any motion
of massive bodies, will give a time-independent field- even if this is the far
field. According to the spirit of GR, a general (time-dependent) gravitation
field should radiate gravitational energy, and here the discussion is less
clear-cut. One often uses the linear approximation of GR and then, as observed
by STEPHANI [28], « if one tries to
calculate not the loss of energy but the total energy of the system emitting
quadrupoles waves, the corresponding integrals diverge for r®¥ if
the system emits continuously (the whole space is filled by radiation). »
Thus in relevant situations which exhibit qualitative differences with NG, the
first-order expansions must be checked by complex expansions. A more severe
difficulty is the contradiction between the principle of general relativity and
the necessity of introducing a flat reference metric, i.e. some equivalent of
the Galilean class of the inertial frames in NG, in order to define a concept
of energy in GR. This difficulty, and some other reasons, led LOGUNOV et al. [14]
to propose a ‘relativistic theory of gravitation’ (RTG), in which the field
equations of GR are supplemented by the De Donder-Fock harmonic condition (Eqs.
(2.39-40) in LOGUNOV et al.
[14]). The RTG is written in generally covariant form, hence the harmonic
condition (2.40) is there an additional
field equation instead of a coordinate condition. Yet the RTG does admit a
privileged class of coordinates (hence also a class of reference frames),
similar to the Galilean class of NG or rather to the Lorentz class of SR. These
are, in the RTG, Galilean coordinates of the ‘base Minkowski space’, i.e. the
space-time equipped with a flat metric g0 [(gmn) in
the notation of LOGUNOV et al.; in the RTG, the metric g0 is
assumed global, and as a consequence of the field equations g0 is
unique]. In such coordinates, as also in coordinates deduced by a linear
transformation, their generally covariant Eq. (2.40) becomes identical to
Fock’s harmonic coordinate condition.
Hence, Galilean coordinates for g0 are also
harmonic coordinates for the ‘effective Riemannian space’, i.e. the space-time
equipped with the curved metric g [(gmn) in their
notations]. A possible objection to the RTG is then, that the arguments leading
to the field equations of GR depend strongly on the equal status enjoyed by all
reference frames: if one has a privileged class of reference frames (exchanging
by Lorentz transformations), one has less physical reasons to express gravity
by generally covariant equations.
4.2 The energy conservation in the studied theory with Newton law
(i) The energy of a free test particle, and its time evolution in
non-static situations
As in NG, the energy of a mass point
appears first as a natural conserved quantity in the case of time-independent
gravitation potential. We have in general from Eq. (2.1) with pe = re c2 and b = pe/pe¥:
(4.9) g = - 
gradg b = gradg U,
U º - c2 Log b .
By the Newton law (3.8) with purely
gravitational force (F0=0),
we have also, using Eq. (3.5):
(4.10) 
where, by definition,
(4.11) 
,
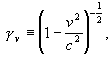v º gt (v,v)1/2 , 
.
To evaluate the rate of work per
unit rest mass, cg.(dx/ds), with g from (4.10), we first observe that
(4.12) 
and, as in Eq. (3.7), we find that
(4.13) 
.
Now, just as in the Lemma in [2] (p.
127), one shows easily with (4.11) that
(4.14) 
.
Accounting for Eqs. (4.12-14), we
thus obtain with (4.10):
,
or, using (4.11):
(4.15) 
+
.
Combining Eqs. (4.9) and (4.15), we
get
(4.16) 
.
In the static case (b,0=0,
whence U,0=0 and g,0=0) we
have thus, coming back to the expression (4.9)2 of U:
(4.17) 
.
But the expression of the (internal
plus kinetic) energy in SR is
(4.18) epm = m(v) c2 = m(0) gv c2,
hence we have get the result that
the total energy of the test particle, including its potential energy in the
gravitation field, is simply
(4.19) em = epm b (= Const. if b,0 = 0).
As in NG, this total energy is lower
than the ‘pure’ energy epm,
in other words the gravitational (potential) energy of matter, egm=em-epm, is negative.
The constancy of em in the
static case is also a result of GR (cf. LANDAU &
LIFCHITZ [12], § 88), since b=(g00)1/2
[Eq. (2.12)]. Yet in GR, this result is not derived from a Newton law and
therefore the evolution of em
in the time-dependent case is complex (moreover, the definition of em, which involves only g00 and
is hence non-covariant, does not make sense in the general case in GR, nor in
the RTG). Here the evolution of em
is simple, especially if l=1/2; by Eq. (4.16) we get:
(4.20) 
+ 
,
(4.21)
+ b gv
, or 
+ 
.
For a light-like particle (photon)
one defines epm=hn with n the
frequency as measured with the local time tx of the momentarily
coincident clock of the frame E, and one then assumes the Newton law (3.8) with epm (or rather epm/c2) in the place of the inertial mass m(v).
Defining also em º b epm for a photon, a
similar way of reasoning[7] shows
that exactly the same balance equation
(4.21)2 is obtained. This extends the result of the static case
[3], i.e. em = Const.
Finally, let us come back to the case of an ordinary free test particle, but
assuming now the space-time geodesic equation Ga=0 of metric g (as
in GR). Using, in the special case where an isopotential coordinate system is
bound to the privileged frame E, the calculation method of ref. [3], one easily
rewrites the ‘time part’ G0=0
as
(4.22) 
.
This is the same as Eq. (4.21) with l=1.
In
summary, if one assumes a Newton law (3.8), then the balance equation (4.21)2
is derived for the total energy em
of any free test particle (mass point or light-like particle), which includes
its potential energy in the gravitation field. Unless l=1/2
is assumed, a term involving both em
and the time-variation of the metric is obtained, which will be seen to be
incompatible with the obtainment of a local conservation equation, i.e. a
balance equation without source term. The value l=1/2 is the only
one for which Leibniz' rule holds true for the vector time derivative (3.5)
entering the Newton law (3.8), but it is incompatible with geodesic motion,
which rather corresponds to l=1.
(ii) The balance equation of energy for dust
We first consider dust, since we
have an expression of the energy balance for a free test particle [Eq. (4.21)].
Dust is a continuum made of non-interacting mass particles, each of which
conserves its rest mass, so that we may use both Eq. (4.21) and the continuity
equation for the density of rest mass, expressing the conservation of the rest mass.
The latter means that the rest mass dm0 contained
within any given ‘substantial’ domain dw of the continuum
is constant, and is thus a statement that can be expressed in terms of any
consistent space and time metric (in so far as the very notion of rest mass is
taken for granted). If we follow the motion of the continuum from the
privileged frame, we can define its velocity v0 with the absolute time, and we can use the volume
measure dV 0 associated
with the natural metric g0 on M, thus
v0 = dx/dt,
dV 0 =
dx1 dx2 dx3.
We then have the usual continuity
equation:
(4.23) 
, r00 ºdm0/ dV 0, div0 º
,
which leads to the following
expression for a ‘substantial’ derivative:
(4.24) 
0
(where the scalar product is of
course g0; but it is true that
g(gradg y, w)= y,i wi
for any metric g and
in any coordinates). We apply this to y = bgv . According to
Eqs. (4.18) and (4.19), y is the (rest) mass density of the
total energy em of dust
matter:
d em = bgv dm0 = r00 bgv dV 0 ºem dV 0,
hence em is the volume density of the energy em in the frame E, the
volume dV 0 being
expressed with ‘uncontracted’ rods, i.e. in terms of the natural metric g0 which
is not affected by gravity. Combining Eqs. (4.21)1 and (4.24), we
get the energy balance for the dust continuum:
(4.25) 
.
It
is necessary to make contact with the mass tensor T, which may be defined for a perfect barotropic fluid as in SR
(and as in GR also), thus (cf. FOCK
[10]):
(4.26) T lm = (m* + p/c2) ul um - (p/c2) g lm , (g lm = d lm),
m* º r*(1 +P / c2), r* = r*(p),
P º 
,
(4.27) ul º dxl/ds
, ul ul =1 and, if x0=ct:
u0=gv /b,
ui=(u0/c) dxi/dt
and the same for the T lm (or Tlm)
components, though with
ul um (or ul um) instead of ul um , and with g lm
(or g lm)
instead of g lm , all indices being raised or
lowered with metric g. Here, r* is the proper
density of rest mass, i.e. the density of rest mass, as measured in a frame C that is bound to the continuum, at least locally and
momentarily (comoving frame). In order to find the connection between r* and
the density of rest mass r0 which would be
evaluated by observers in the frame E, one just has to
use SR which holds true locally. The local observers in E and
in C relate their
space and time measurements by local Lorentz transformation, hence the
measures, in E, of the ‘substantial’ volume element in C and the mass density are
(4.28) dVE = dVC /gv , r0 
= gv
= gv r*
(note that the observer in E uses the ‘true’ simultaneity, hence he finds
the same relation dVE = dVC /gv if he simply
remembers that the measuring rods of the observer in C are
‘truly’ Lorentz-contracted in direction v).
Since the physical metric g in the frame E is affected by gravitational contraction of
measuring rods, the corresponding volume dVE
is dilated with respect to the volume dV 0 expressed in terms of the natural
metric [cf. Eq. (2.7)], thus from (4.23) and (4.28):
(4.29) dV 0 = b dVE , r00 = r0/b = gv r*/b .
Now, from Eqs. (4.26) and (4.27), we
have for dust (p=0, P=0):
r* gv2 = (T 00)E , r* gv2 v0i/c = (T i0)E (x0=ct),
whatever space coordinates bound to E are used; indeed, one has always g0i =0 in such coordi-nates
[see Eq. (2.8)], hence u0 u0 = g00(u0)2 =gv2. By
(4.29), we have r* gv2 = r00 gv b = em , hence we may
rewrite the balance equation (4.25) as:
(4.30)
where x0=ct, the
space coordinates are bound to E, and the space-time metric g0 is
defined by
(ds0)2=(dx0)2-(dl 0)2
with dl 0 the line element of the natural space metric g0; the
first identity is valid in any
coordinates linearly bound to Galilean coordinates of the metric g0 [if (M, g0) is Euclidean.
Except for the first identity, Eq. (4.30) is yet valid also if (M, g0) is a space with
constant curvature].
Equation
(4.30) [or (4.25)] still contains the two source terms on the right-hand side.
If it transforms into a true conservation equation, this must include the
energy of the gravitation field itself. As
in NG, we have to use the field equation in order to replace the energy
density by a combination of derivatives of the potential [here fºb 2, with
b=pe/pe¥, is
the exact analogue of the Newtonian potential, Eq. (2.12)]. However,
it remains some ambiguity as regards the precise definition of the mass-energy
density r in the field equation (2.2) or (2.15): is that T 00, T 00 or T 00 ? To answer this
question, we will precisely impose the condition that a conservation equation
must be obtained, and we will check the interpretation of r by
the physical consequences of this interpretation. In the case where the model
of universe is static at infinity, in the rather wide sense [see after Eq.
(2.13)] that pe¥ does
not depend on the time t, we may use
the field equation in the form (2.15). We obtain from (2.15) and (2.12), by
using (locally) Cartesian coordinates (i.e. g0ij=dij and g0ij,k =0 at
the considered point):
(4.31)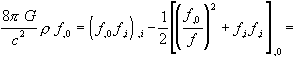 
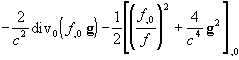
[where the scalar square g2 is in terms of the
natural metric, g2=g0(g,g)].
This strongly recalls the ‘pure gravitational’ terms in the Newtonian Eq.
(4.2), though with an additional term (f,0/f)2. Now we observe that the
first source term on the right of Eq. (4.30) can be written as
(4.32) 
.
Hence, if we interpret the
mass-energy density r as T 00, and if we demand that Leibniz’ rule applies to the
definition of a vector time derivative, i.e. l=1/2 in Eqs.
(3.5) and (3.8), then we obtain for dust, from Eqs. (4.30-32), the following conservation equation for the energy:
(4.33)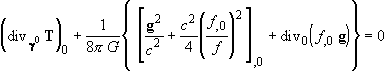 
.
As will be seen, the interpretation
of r as T 00 means that the
gravitation field definitely reinforces itself and is thus very plausible.
Other possible interpretations: r = T 00 or r = T 00, certainly do
not allow to rewrite the energy balance (4.30) as a true conservation equation
if l=1/2
[because one then adds to Eq. (4.33) the term
f,0(T 00- r)/2,
which is clearly not a 4-divergence]. Finally, if a different value is assumed
for l, not
only Leibniz’ rule fails to apply, but the mixed source term [the last term in
Eq. (4.30)] makes it more than unlikely that a conservation equation could be
obtained for the energy. Thus we assume
l=1/2 and r = T 00 from now on.
(iii) Extension of the energy conservation equation to general
matter behaviour
For general matter behaviour, the
constitutive material particles interact with each other and do not necessarily
conserve their rest mass. Still, other conservation laws of microphysics hold
true in rather general situations, in particular that for the baryon number
which was proposed by CHANDRASEKHAR [8]
as a substitute for the mass conservation. However, it is considered here that
no conservation law is more fundamental than that for energy. Equation (4.33)
applies in the absence of gravitation, i.e. in SR, with T the mass tensor of any kind of matter and field {incidentally,
matter and non-gravitational fields would be of similar nature, i.e. all these
would be microscopic flows in ether, according to the concept of constitutive
ether (cf. ROMANI [24])}. In the presence of gravity, Eq. (4.33) has
been derived, for dust, from the assumed conservation of the rest mass. We
therefore postulate that Eq. (4.33) holds true with T the (mixed) mass tensor of any kind of matter and
non-gravitational field, in the presence of gravitation. Since the total
energy, not the rest mass, is thereby conserved, this postulate contains the
possibility that (depending on the constitutive equation) matter can be created or destroyed by its interaction with a variable
gravitation field.
(iv) Some local and global consequences of the conservation equation
The density of pure gravitational
energy (or rather of its mass equivalent), with respect to the natural volume
measure dV 0, appears
clearly in Eq. (4.33); it is
(4.34)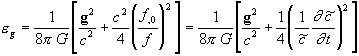 
,
where 
º dl 0/dt = cf [cf. Eqs. (2.5) and
(2.7)] is the ‘absolute’ velocity of light (and that of waves of the pressure pe , i.e. gravitation waves)
in the direction g. Comparing with
the Newtonian gravitational energy wg
[Eq. (4.2)], we see that the studied theory, in which the metric varies with
time, says that this variation demands energy. On the other hand, it is
recalled that the energy density of matter, T
00 with
(4.35) T 00=em ( = r00 gv b for dust),
which also is relative to dV 0, and which enters the
balance equation (4.33), includes its ‘potential’ energy in the gravitation
field [cf. Eqs. (4.18-19)]. Let us examine, in the static case, what follows
from assuming that r on the r.h.s. of the field equation
(2.15) is
T 00 =T 00/b 2 (as
is imposed if one admits that a conservation equation must exist for energy).
Since the density of the ‘pure’ energy of matter, i.e. without its potential
energy, is
epm = T 00/b
(again with respect to dV 0),
it means that
r = epm/b. Due to the ‘Poisson equation’
(2.15) with f,0=0, Eq.
(2.16) determines in the general static case the ‘active mass’ m, giving the expression (2.9) of the
space-time metric: at large distance from the massive body (which is unique,
since any other body would fall, and which is at rest in the ether), we have
approximate spherical symmetry, hence
(4.36) f = 1- 2 Gm/(c2r) + o(1/r)
(r
being the Euclidean distance from the body), with
(4.37) m = òbody r dV 0
= òbody (epm/b) dV 0
This means that the density epm of the ‘pure’
(internal plus kinetic) energy is reinforced, as regards its contribution to
the ‘active gravitational’ mass m, in
the very proportion of the local gravitation field b<1, i.e. the gravitation field reinforces itself,
as desired. If, instead of
r = T 00,
we would assume
r =T 00 or r =T
00,
we would get epmb or epmb 3
in the place of epm/b in Eq. (4.37), i.e. the gravitation field
would have a weakening effect on
itself. But the notion of active mass, especially its comparison with the
passive gravitational mass [which is also the inertial mass, and still
coincides with the pure energy of matter, cf. the Newton law (3.8) and Eqs.
(4.18-19)], implies a linearity of the acceleration field g with respect to the amount of matter. This amount is best
represented by the pure energy of matter, thus its density epm does not
coincide with r. The scalar f depends non-linearly on the distribution of epm, even in the
static case [Eq. (2.15) with
r = epm/b], hence the same is true for the
vector g [Eq. (2.12)]. One therefore
cannot isolate the gravitation force exerted by a subdomain W on a
mass point, i.e. the contribution of W to the field g. Hence, an actio-reactio principle cannot even be defined for the
gravitation force, even in the static case. In summary, the studied theory
implies (at least in the static case) that the gravitation field really
reinforces itself, and this forbids to define the active gravitational mass for
a subdomain of the system. As to the global active mass, it may be defined, at
least in the static case, and it is then greater than the sum of the pure
energy of matter, for the same reason.
In
the more general situation of an isolated, but not necessarily static matter
distribution, embedded in Euclidean
space M, the integration of Eq.
(4.33) over the whole space and its transformation is possible, under the
sufficient condition that (f,0)2
is o(1/r3) and g is O(1/r2)
at large r (with r the current Euclidean distance from some point in the group of
bodies, and using the fact that f »1 at
large r. In assuming that the
behaviour at large r is as in NG, one
indeed would expect this decrease of g
like 1/r2; actually, this
is not the general case, due to the gravitation waves). Using Gauss’ theorem on
the sphere r=R and making R tend towards +¥, we
obtain then
(4.38) Wm + Wg
º òmatter em dV 0 + òspace eg dV 0 = Const. = W,
which is the same as Eq. (4.3),
though here em and eg are given by
Eqs. (4.35) and (4.34). Due to the presence of the term (f,0/f)2
in eg, the reduction
of the second integral to an integral restricted to matter seems possible only
in the static case. We have then from (2.12) and (2.15):
(4.39) 
.
At large r, we have Eq. (4.36) plus g
» - (G m / r2) er (with er the unit
radial vector, and where » means ‘equivalent to’), whence from (4.34) and (4.39)
by using Gauss’ theorem on the sphere r=R
and making R tend towards +¥:
Wg º òspace eg dV 0 = (m - òbody r f dV 0)/4.
Since em = r f = epmb (= T 00), we can thus
rewrite the conserved energy, in the static situation (which may be the case
for the initial, as well as for the final state), as
(4.40)
W = 
òbody em dV 0 + 
òbody 
dV 0.
(4.41)
It is smaller than the active mass m [Eq.(4.37)], and the latter does not
need to remain the same in any couple of initial and final states, both being
assumed static. Furthermore, and in contrast with NG [see the discussion after
Eq. (4.4)], the structure of Eq. (4.40) does not seem to imply that the pure
energy of matter,
òmatter epm dV 0 ,
is necessarily increased as the pure gravitational energy Wg is increased, i.e. in the
case of gravitational concentration of matter.
5. Conclusion
Although less immediately than in
the case of a static gravitation field, a consistent Newton law can still be
defined in the general situation within the present theory (and in fact in any
theory which, in a reference frame, provides us with a space metric and a time
metric). It is consistent in that it is based on a true vector derivative of
the momentum, obeying Leibniz’ rule with the variable metric g (here
g is the physical space metric in the privileged frame
bound to ether); moreover, this time derivative coincides with the usual
absolute derivative in the case of a time-independent metric g, i.e.
in the static case. The requirement that Leibniz’ rule must hold true permits
to select the relevant vector derivative, i.e. l=1/2 in Eq.
(3.5), from a one-parameter family of candidates. Among the possibilities which
are thereby eliminated, the value l=1 is likely to correspond to
Einstein's motion along space-time geodesics; anyhow, l=1
does correspond to geodesic motion in the important case where ‘isopotential’
coordinates bound to ether still exist (see the definition near Eq. (2.7); this
case includes spherical symmetry around a point bound to ether). A general
Newton law is important for the status of the theory, since it means that the
acceleration field g [Eq. (2.1)]
keeps a direct physical meaning in the most general case. Thus the above result
implies a crucial departure of the theory from the ‘logic of space-time’. The
latter is the commonly accepted interpretation
of SR, even though the ‘logic of absolute motion’ can be vindicated as well in
SR [4, 6-7, 11, 21-23]. The logic of space-time is, however, essential in GR, and even also in its
various formulations or modifications as a field theory in flat space-time
(including the theory proposed by LOGUNOV et al. [14]).
It
seems therefore natural to hesitate before taking the new direction at this
bifurcation in the studied theory. But another argument leads to the same
choice, and this is not quite a detail: if one wants to have a true
conservation equation for energy in this theory, one also must assume the
Newton law (with Leibniz’ rule, thus l=1/2) and hence forget space-time
geodesics. One then indeed obtains for energy a local balance equation without
source term, and this is in terms of a flat space-time metric. The
gravitational energy is thereby unambiguously defined (in contrast with GR).
Just like in NG, one must recognize that one part of gravitational energy is
embedded in matter, as its (negative) potential energy in the gravitation
field, while the other (positive) part is present in the whole space and may be
called the pure gravitational energy. The expression of the latter in the
present theory [Eq. (4.34)] contains just the Newtonian expression, plus a term
bound to the fact that any time-dependence of the gravitation field implies a
time-dependence of the local space and time standards: according to the studied
theory, such variation demands an energy supply. This feature of the theory
will be worth to discuss in connection with the question of gravitation waves.
When the local balance equation can be integrated (which is not the case if
gravitation waves are filling the space), it implies the conservation of the
global energy [Eq. (4.38)], which is the sum of the energy of matter (including
its negative potential energy) and the pure gravitational energy. The
gravitation field does reinforce itself in a direct sense [Eq. (4.37)].
According
to the present ether theory, gravitation would have some rather concrete
aspects. But it is once again emphasized that the theory is non-covariant,
which is a risk as regards its application to celestial mechanics. One thus has
to study what would be the effect, say on the motion of a planet considered as
a test particle, of a uniform motion
of the attracting body. This effect will be at most in u2/c2
with u the corresponding constant
velocity. It is therefore expected that the perturbation of the Newtonian
analysis is small enough so that the theory, at least, is not worse than NG for mechanics of the solar
system, except perhaps for time scales beyond the ‘horizon of predictibility’
implied by chaotic behaviour of N-bodies problems. It might happen, however,
that (due to the effect of the velocity u),
the theory could fail to account for such very small effects as the advance of
perihelion of Mercury, i.e. it could fail to improve NG in that respect (the
motion of the perihelion is very sensitive to almost any kind of perturbation).
As to the gravitational red shift, the deflection of light rays and the delay
of radar signals, it seems plausible that the effect of the velocity u does not change significantly their
magnitude, which would thus be correctly predicted. The writer has already
verified this point as regards the red shift.
ACKNOWLEDGEMENTS
I am very grateful to Profs. P.
Guélin and E. Soós for discussions which helped me to realize that a consistent
energy concept is even more necessary in a non-covariant theory like the
present one.
REFERENCES
1. M. ARMINJON, A theory of
gravity as a pressure force. I. Newtonian space and time, Rev. Roum. Sci.
Tech.-Méc. Appl. 38, 3-24, 1993.
2. M. ARMINJON, A theory of
gravity as a pressure force. II. Lorentz contraction and ‘relativistic’ effects, Rev. Roum. Sci. Tech.-Méc. Appl.
38, 107-128, 1993.
3. M. ARMINJON, Scalar theory of
gravity as a pressure force, submitted to Z. Naturforsch.a
4. J.S. BELL, How to teach special
relativity, in: Speakable and unspeakable in quantum mechanics, pp. 67-80.
Cambrige University Press, Cambridge, 1987.
5. L. BRILLOUIN, Les tenseurs en mécanique et en élasticité,
Masson, Paris, 1949.
6. G. BUILDER, Ether and Relativity, Austr. J. Phys. 11, 279-297, 1958.
7. G. BUILDER, The constancy
of the velocity of light, Austr. J. Phys. 11, 457-480, 1958.
8. S. CHANDRASEKHAR, Conservation
laws in general relativity and in the post-Newtonian approximations,
Astrophys. J. 158, 45, 1969.
9. V.P. DMITRYIEV, Particles and
fields in the vortex sponge, Z. Naturforsch. 48a, 935-942, 1993.
10. V. FOCK, The theory of space,
time and gravitation, Pergamon, Oxford, 1964.
11. L. JANOSSY, The Lorentz
principle, Acta Physica Polonica 27,
61-87 (1965).
12. L. LANDAU, E. LIFCHITZ, Théorie des champs (3rd
french edition), Mir, Moscow, 1970.
13. A. LICHNEROWICZ, Eléments de calcul tensoriel, Armand
Colin, Paris, 1950.
14. A.A. LOGUNOV, Yu.M. LOSKUTOV, M.A. MESTVIRISHVILI, The relativistic theory of gravitation and
its consequences, Sov. Phys. Usp. 31,
581-596, 1988 (Transl. from Usp. Fiz. Nauk 155, 369-396, 1988).
15. E. MADELUNG, Quantentheorie in
hydrodynamischer Form, Z. Physik 40,
322, 1926.
16. P. MAZILU, Missing link in the
theory of gravity interaction, Proc. 6th. Marcel Grossmann Meet. Gen.
Relat. (H. Sato & T. Nakamura, eds.), World Scientific, 1992.
17. D. MERMIN, Hidden variables
and the two theorems of John Bell, Rev. Modern Phys. 65, 803-815, 1993.
18. J.R. OPPENHEIMER, H. SNYDER, Phys. Rev. 56, 455, 1939.
19. J.P. OSTRIKER, Astronomical
tests of the cold dark matter scenario, Ann. Rev. Astron. Astrophys. 31, 689-716, 1993.
20. R. PENROSE, Gravitational
collapse and space-time singularities, Phys. Rev. Lett. 14, 57-59, 1965.
21. S.J. PROKHOVNIK, The logic of
special relativity, Cambridge University Press, Cambridge, 1967.
22 S.J. PROKHOVNIK, The general
solutions of the Robertson-Walker null-geodesic and their implications, Z.
Naturforsch. 48a, 915-924, 1993.
23 S.J. PROKHOVNIK, The physical
interpretation of special relativity - a vindication of Hendrik Lorentz, Z.
Naturforsch. 48a, 925-931, 1993.
24. L. ROMANI, Théorie générale de l'univers physique
(2 vols.), Librairie Scientifique A. Blanchard, Paris, 1975 and 1976.
25. D. SCIAMA, The physical
significance of the vacuum state of a quantum field, in: The Philosophy of
Vacuum (S. Saunders & H.R. Brown, eds.), pp.137-158, Clarendon Press,
Oxford, 1991.
26. E. SOÓS, Géométrie et électromagnétisme,
published by Seminarul de Mecanica (V. Obadeanu, ed.), University of Timisoara,
Romania, 1992.
27. N. STAVROULAKIS, Sur le principe d’équivalence et le problème
de l’énergie, Ann. Fondation L. de Broglie 18, 221-230, 1993.
28. H. STEPHANI, General
Relativity, Cambridge University Press, Cambridge, 1982.
29. A. TRAUTMAN, Sur les lois de conservation dans les
espaces de Riemann, in: Les Théories Relativistes de la Gravitation, pp.
113-116, Ed. du CNRS, Paris, 1962.
30. V. TRIMBLE, Existence and
nature of dark matter in the universe, Ann. Rev. Astron. Astrophys. 25, 425-472, 1987.
31. F. WINTERBERG, Substratum
approach to a unified theory of elementary particles, Z. Naturforsch. 43a, 1131-1150,1988.
32. F. WINTERBERG, The occurrence
of a finite number of particle families in the Planck aether model of a unified
field theory, Z. Naturforsch. 46a, 677-685, 1991.
Laboratoire
‘Sols, Solides, Structures’ [associated with the Centre National de la
Recherche Scientifique], Institut de Mécanique de Grenoble, B.P. 53 X, F-38041
Grenoble cedex, France.